题目内容
【题目】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程.
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
【答案】(1) y=(2±![]() )x或x+y+1=0或x+y-3=0;(2)
)x或x+y+1=0或x+y-3=0;(2) ![]()
【解析】
(1)首先利用待定系数法设出切线的方程,然后利用圆心到切线的距离等于半径求出切线方程;(2)PM的距离用P到圆心C的距离与半径来表示,建立PO与与PC的关系,求出P点的轨迹为一条直线,然后将求PM的最小值问题转化为原点到直线的距离问题,
解:(1)将圆C整理得(x+1)2+(y-2)2=2.
①当切线在两坐标轴上的截距为零时,设切线方程为y=kx,
∴圆心到切线的距离为![]() ,即k2-4k-2=0,解得k=2±
,即k2-4k-2=0,解得k=2±![]() .
.
∴y=(2±![]() )x;
)x;
②当切线在两坐标轴上的截距不为零时,设切线方程为x+y-a=0,
∴圆心到切线的距离为![]() ,即|a-1|=2,解得a=3或-1.
,即|a-1|=2,解得a=3或-1.
∴x+y+1=0或x+y-3=0.综上所述,所求切线方程为y=(2±![]() )x或x+y+1=0或x+y-3=0.
)x或x+y+1=0或x+y-3=0.
(2)∵|PO|=|PM|,
∴![]() =(x1+1)2+(y1-2)2-2,即2x1-4y1+3=0,即点P在直线l:2x-4y+3=0上.
=(x1+1)2+(y1-2)2-2,即2x1-4y1+3=0,即点P在直线l:2x-4y+3=0上.
当|PM|取最小值时,即|OP|取得最小值,此时直线OP⊥l,
∴直线OP的方程为:2x+y=0,
解得方程组![]() 得
得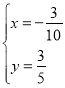 ,
,
∴P点坐标为![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目