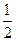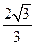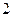题目内容
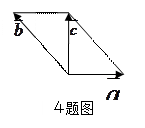
已知a、b是两个非零向量,当a+tb(t∈R)的模取最小值时,
(1)求t的值;
(2)求证:b⊥(a+tb).
(1)求t的值;
(2)求证:b⊥(a+tb).
(1)设
与
的夹角为θ,
∵|
+t
|2=(
+t
)2=|
|2+t2|
|2+2
•(t
)=|
|2+t2|
|2+2t|
||
|cosθ
=|
|2(t+
cosθ)2+|
|2sin2θ,
∴当t=-
cosθ=-
=-
时,|
+t
|有最小值.
(2)证明:∵
•(
+t
)=
•(
-
•
)=
•
-
•
=0,
∴
⊥(
+t
).
| a |
| b |
∵|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
=|
| b |
|
| ||
|
|
| a |
∴当t=-
|
| ||
|
|
| |a||b|cosθ |
| |b|2 |
| ||||
|
|
| a |
| b |
(2)证明:∵
| b |
| a |
| b |
| b |
| a |
| a•b |
| |b|2 |
| b |
| a |
| b |
| a |
| b |
∴
| b |
| a |
| b |

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
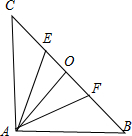
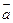 与向量
与向量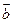 的夹角为
的夹角为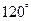 ,若向量
,若向量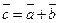 ,且
,且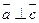 ,
,
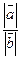 的值为 ( )
的值为 ( )