题目内容
设椭圆的方程为 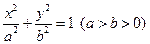 , 线段
, 线段 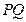 是过左焦点
是过左焦点 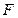 且不与
且不与 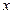 轴垂直的焦点弦. 若在左准线上存在点
轴垂直的焦点弦. 若在左准线上存在点 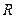 , 使
, 使 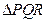 为正三角形, 求椭圆的离心率
为正三角形, 求椭圆的离心率 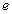 的取值范围, 并用
的取值范围, 并用 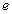 表示直线
表示直线 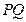 的斜率.
的斜率.
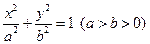 , 线段
, 线段 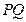 是过左焦点
是过左焦点 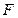 且不与
且不与 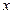 轴垂直的焦点弦. 若在左准线上存在点
轴垂直的焦点弦. 若在左准线上存在点 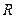 , 使
, 使 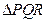 为正三角形, 求椭圆的离心率
为正三角形, 求椭圆的离心率 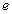 的取值范围, 并用
的取值范围, 并用 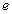 表示直线
表示直线 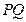 的斜率.
的斜率. 
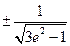
如图, 设线段 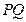 的中点为
的中点为 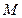 .过点
.过点 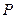 、
、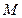 、
、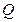 分别作准线的垂线, 垂足分别为
分别作准线的垂线, 垂足分别为 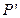 、
、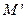 、
、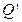 , 则
, 则


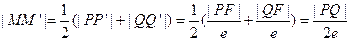 . …………… 6分
. …………… 6分
假设存在点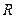 ,则
,则 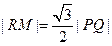 , 且
, 且  , 即
, 即 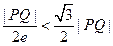 ,所以,
,所以,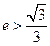 .……… 12分.
.……… 12分.
于是,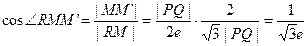 , 故
, 故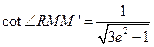 .
.
若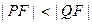 (如图),则
(如图),则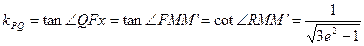 . … 18分
. … 18分
当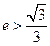 时, 过点
时, 过点 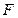 作斜率为
作斜率为 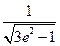 的焦点弦
的焦点弦 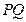 , 它的中垂线交左准线于
, 它的中垂线交左准线于 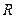 , 由上述运算知,
, 由上述运算知, 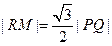 . 故
. 故 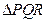 为正三角形. ………… 21分
为正三角形. ………… 21分
若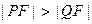 ,则由对称性得
,则由对称性得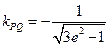 . ……………… 24分
. ……………… 24分
又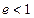 , 所以,椭圆
, 所以,椭圆 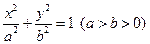 的离心率
的离心率 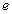 的取值范围是
的取值范围是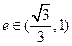 , 直线
, 直线 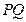 的斜率为
的斜率为 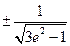 .
.
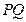 的中点为
的中点为 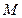 .过点
.过点 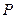 、
、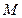 、
、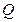 分别作准线的垂线, 垂足分别为
分别作准线的垂线, 垂足分别为 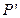 、
、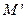 、
、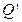 , 则
, 则

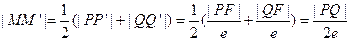 . …………… 6分
. …………… 6分假设存在点
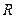 ,则
,则 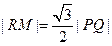 , 且
, 且  , 即
, 即 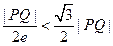 ,所以,
,所以,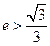 .……… 12分.
.……… 12分.于是,
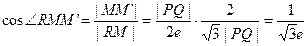 , 故
, 故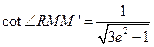 .
.若
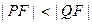 (如图),则
(如图),则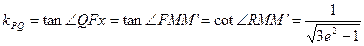 . … 18分
. … 18分当
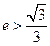 时, 过点
时, 过点 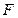 作斜率为
作斜率为 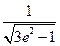 的焦点弦
的焦点弦 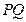 , 它的中垂线交左准线于
, 它的中垂线交左准线于 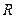 , 由上述运算知,
, 由上述运算知, 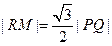 . 故
. 故 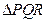 为正三角形. ………… 21分
为正三角形. ………… 21分若
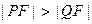 ,则由对称性得
,则由对称性得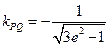 . ……………… 24分
. ……………… 24分又
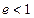 , 所以,椭圆
, 所以,椭圆 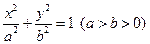 的离心率
的离心率 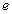 的取值范围是
的取值范围是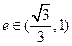 , 直线
, 直线 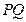 的斜率为
的斜率为 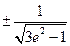 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =1的左焦点,Q是椭圆上任一点,P点分
=1的左焦点,Q是椭圆上任一点,P点分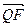 的比为2,则P的轨迹方程为_________________.
的比为2,则P的轨迹方程为_________________. 的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点
的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点 ,向量
,向量 与
与 是共线向量。
是共线向量。 分别是左、右焦点,求∠
分别是左、右焦点,求∠ 的取值范围;
的取值范围;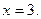 (I)求椭圆C的方程; (II)过点F作斜率为k的直线l,与椭圆C交于A、B两点,若
(I)求椭圆C的方程; (II)过点F作斜率为k的直线l,与椭圆C交于A、B两点,若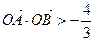 ,求k的取值范围。
,求k的取值范围。 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点 也在椭圆上,且满足
也在椭圆上,且满足 (
( 为坐标原点),
为坐标原点), .若椭圆的离心率等于
.若椭圆的离心率等于 .
. 的方程;
的方程; 的面积等于
的面积等于 ,求椭圆的方程.
,求椭圆的方程. 的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.
的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.  ,一个焦点是F(-m,0)(m是大于0的常数).
,一个焦点是F(-m,0)(m是大于0的常数). |=2|
|=2| |,求直线l的斜率.
|,求直线l的斜率.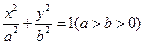 的左焦点
的左焦点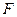 任作一条与两坐标轴都不垂直的弦
任作一条与两坐标轴都不垂直的弦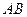 ,若点
,若点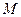 在
在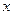 轴上,且使得
轴上,且使得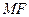 为
为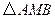 的一条内角平分线,则称点
的一条内角平分线,则称点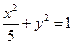 的“左特征点”
的“左特征点” 的内部,则m的取值范围是 ( )
的内部,则m的取值范围是 ( ) <m<
<m<