题目内容
18. 如图,PA切⊙O于点A,割线PBC经过圆心O,PB=1,PA=$\sqrt{3}$,OA绕点O逆时针旋转60°到OD,则PD的长为$\sqrt{7}$.
如图,PA切⊙O于点A,割线PBC经过圆心O,PB=1,PA=$\sqrt{3}$,OA绕点O逆时针旋转60°到OD,则PD的长为$\sqrt{7}$.
分析 法一:如图根据题设条件可求得角DOP的大小,由于OD=1,OP=2,由余弦定理求长度即可.
法二:由图形知,若能求得点D到线段OC的距离DE与线段OE的长度,在直角三角形PED中用勾股定理求PD即可.
解答 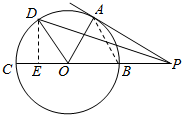 解法一:∵PA切⊙O于点A,B为PO中点,
解法一:∵PA切⊙O于点A,B为PO中点,
∴AB=OB=OA,
∴∠AOB=60°,∴∠POD=120°,
在△POD中由余弦定理,
得:PD2=PO2+DO2-2PO•DOcos∠POD=4+1-4×(-$\frac{1}{2}$)=7,
∴PD=$\sqrt{7}$.
解法二:过点D作DE⊥PC垂足为E,
∵∠POD=120°,
∴∠DOC=60°,
可得OE=$\frac{1}{2}$,DE=$\frac{\sqrt{3}}{2}$,
在Rt△PED中,有PD=$\sqrt{P{E}^{2}+D{E}^{2}}$=$\sqrt{\frac{25}{4}+\frac{3}{4}}$=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考点是与圆有关的比例线段,本题考查求线段的长度,平面几何中求线段长度一般在三角形中用正弦定理与余弦定理求解,做题后要注意总结方法选取的规律.

练习册系列答案
相关题目
9.数列{an}满足an+an+1=$\frac{1}{2}$(n∈N,n≥1),若a2=1,Sn是{an}的前n项和,则S21的值为( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{9}{2}$ | D. | -$\frac{9}{2}$ |
13.将函数y=sin(2x-$\frac{π}{3}$)的图象向右平移$\frac{7π}{12}$个单位,再将图象上每个点的横坐标扩大到原来的2倍,纵坐标不变,得到的图象对应的函数表达式是( )
| A. | y=sin(x+$\frac{5}{6}$π) | B. | y=cosx | C. | y=sin(4x+$\frac{5}{6}$π) | D. | y=cos4x |
10.命题“对任意的x∈R,x2≥0”的否定是( )
| A. | 对任意的x∈R,x2<0 | B. | 不存在x∈R,x2<0 | ||
| C. | 存在x∈R,x2<0 | D. | 存在x∈R,x2≥0 |
7.下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A. | y=cos2x,x∈R | B. | y=x3+1,x∈R | ||
| C. | y=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R | D. | y=log2|x|,x∈R且x≠0 |