题目内容
4.设函数$f(x)=2cos(\frac{1}{2}x+\frac{π}{6})$,则该函数的最小正周期为4π,值域为[-2,2],单调递增区间为[4kπ-$\frac{7π}{3}$,4kπ-$\frac{π}{3}$],k∈z.分析 由条件根据函数y=Asin(ωx+φ)的周期性、值域和单调性,可得结论.
解答 解:函数$f(x)=2cos(\frac{1}{2}x+\frac{π}{6})$的该函数的最小正周期为$\frac{2π}{\frac{1}{2}}$=4π,值域为[-2,2].
令2kπ-π≤$\frac{1}{2}$x+$\frac{π}{6}$≤2kπ,求得4kπ-$\frac{7π}{3}$≤x≤4kπ-$\frac{π}{3}$,
故函数的减区间为[4kπ-$\frac{7π}{3}$,4kπ-$\frac{π}{3}$],k∈z.
故答案为:$4π;[-2,2];[4kπ-\frac{7π}{3},4kπ-\frac{π}{3}],k∈$Z.
点评 本题主要考查函数y=Asin(ωx+φ)的周期性、值域和单调性,属于基础题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
12.下列函数中,在其定义域上既是奇函数又是增函数的是( )
| A. | y=logax | B. | y=x3+x | C. | y=3x | D. | y=-$\frac{1}{x}$ |
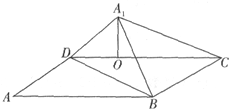 如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.
如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.