题目内容
19．若角α的终边落在直线x+y=0上，求在[-360°，360°]内的所有满足条件的角α．分析 求出角α的终边相同的角，然后求解在[-360°，360°]内的所有满足条件的角α．
解答 解：角α的终边落在直线x+y=0上，则直线的倾斜角为：45°，
角α的终边的集合为：{α|α=k•180°+45°，k∈Z}．
当k=-2时，α=-315°，k=-1时，α=-135°，
k=0时，α=45°，k=1时，α=225°，
在[-360°，360°]内的所有满足条件的角α：-315°，135°，45°，225°．
点评 本题考查终边相同角的表示，考查计算能力．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
9．若x，y＞0，且x+2y=1，则（x+$\frac{1}{x}$）（y+$\frac{1}{4y}$）的最小值是（ ）
| A． | $\frac{25}{2}$ | B． | $\frac{25}{4}$ | C． | $\frac{25}{8}$ | D． | $\frac{25}{16}$ |
7．已知点A（cos77°，sin77°），B（cos17°，sin17°），则直线AB的斜率为（ ）
| A． | tan47° | B． | tan43° | C． | -tan47° | D． | -tan43° |
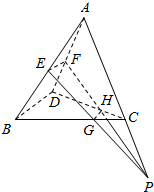已知空间四边形ABCD中，E，F分别是AB，AD的中点，G，H分别是BC，CD上的点，且$\frac{BG}{GC}=\frac{DH}{HC}$=2，求证：直线EG，FH，AC相交于同一点P．