题目内容
13．若关于x的方程lg3x×lg4x-a2=0有两个不相等的实数根，则方程的两根之积为$\frac{1}{12}$．分析 先根据对数的运算性质，化简得到lg3lg4+（lg3+lg4）lgx+lg2x-a2=0，设设方程的两根为x1，x2，根据韦达定理即可求出．
解答 解：lg3x×lg4x-a2=（lg3+lgx）（lg4+lgx）-a2=lg3lg4+（lg3+lg4）lgx+lg2x-a2=0
设方程的两根为x1，x2，
∴两根之和为lgx1+lgx2=lgx1x2=-（lg3+lg4）=-lg12=lg$\frac{1}{12}$
所以x1x2=$\frac{1}{12}$，
故答案为：$\frac{1}{12}$
点评 本题考查韦达定理和对数的运算性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
4．若函数f（x）=x2-2kx+5在[2，4]上具有单调性，则实数k的取值范围是（ ）
| A． | [4，+∞） | B． | （-∞，-2] | C． | [2，+∞） | D． | （-∞，2]∪[4，+∞） |
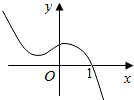已知函数y=f（x）的图象如图，则满足$f（{\frac{{2{x^2}-x-1}}{{{x^2}-2x+1}}^{\;}}）•f（2）≤0$的x的取值范围[-2，1）．