题目内容
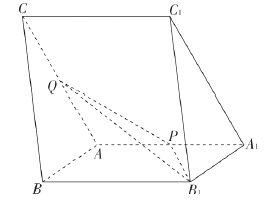
【题目】如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1 , 这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面. 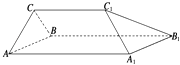
【答案】解:这个几何体不是棱柱,截去的部分是一个四棱锥C1﹣EA1B1F, 如图所示;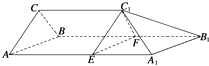
在四边形ABB1A1中,在AA1上取点E,使AE=2,
在BB1上取F使BF=2;
连接C1E,EF,C1F,
则过C1EF的截面将几何体分成两部分,其中一部分是棱柱ABC﹣EFC1 , 其棱长为2;
截去的部分是一个四棱锥C1﹣EA1B1F.
【解析】
【考点精析】认真审题,首先需要了解平面的基本性质及推论(如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线).

练习册系列答案
相关题目