题目内容
(本小题满分12分)在如图所示的几何体中,四边形ABCD为平行四边形,∠ ACB= ,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE
,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE
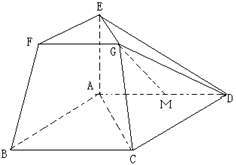
 ,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE
,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE 
见解析。
本题考查线面平行的判定定理。
根据所给的一系列平行,得到三角形相似,根据平行四边形的判定和性质,得到线与线平行,根据线与面平行的判定定理,得到线面平行.
证法一:
因为EF//AB,FG//BC,EG//AC,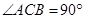 ,
,
所以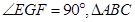 ∽
∽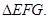
由于AB=2EF,因此,BC=2FG,
连接AF,由于FG//BC,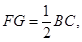 ----------6分
----------6分
在 中,M是线段AD的中点,
中,M是线段AD的中点,
则AM//BC,且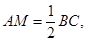 因此FG//AM且FG=AM,所以四边形AFGM为平行四边形,因此GM//FA。又
因此FG//AM且FG=AM,所以四边形AFGM为平行四边形,因此GM//FA。又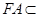 平面ABFE,
平面ABFE,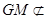 平面ABFE,
平面ABFE,
所以GM//平面AB。---------------12分
证法二:
因为EF//AB,FG//BC,EG//AC,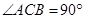 ,
,
所以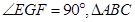 ∽
∽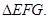 由于AB=2EF,
由于AB=2EF,
因此,BC=2FC,取BC的中点N,
连接GN,因此四边形BNGF为平行四边形,所以GN//FB,---------6分
在 中,M是线段AD的中点,连接MN,则MN//AB,
中,M是线段AD的中点,连接MN,则MN//AB,
因为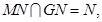 所以平面GMN//平面ABFE。又
所以平面GMN//平面ABFE。又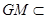 平面GMN,
平面GMN,
所以GM//平面ABFE。-----------------------------------------12分
根据所给的一系列平行,得到三角形相似,根据平行四边形的判定和性质,得到线与线平行,根据线与面平行的判定定理,得到线面平行.
证法一:
因为EF//AB,FG//BC,EG//AC,
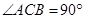 ,
,所以
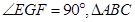 ∽
∽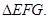
由于AB=2EF,因此,BC=2FG,
连接AF,由于FG//BC,
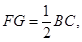 ----------6分
----------6分在
 中,M是线段AD的中点,
中,M是线段AD的中点,则AM//BC,且
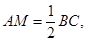 因此FG//AM且FG=AM,所以四边形AFGM为平行四边形,因此GM//FA。又
因此FG//AM且FG=AM,所以四边形AFGM为平行四边形,因此GM//FA。又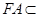 平面ABFE,
平面ABFE,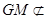 平面ABFE,
平面ABFE,所以GM//平面AB。---------------12分
证法二:
因为EF//AB,FG//BC,EG//AC,
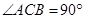 ,
,所以
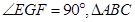 ∽
∽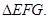 由于AB=2EF,
由于AB=2EF,因此,BC=2FC,取BC的中点N,
连接GN,因此四边形BNGF为平行四边形,所以GN//FB,---------6分
在
 中,M是线段AD的中点,连接MN,则MN//AB,
中,M是线段AD的中点,连接MN,则MN//AB,因为
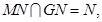 所以平面GMN//平面ABFE。又
所以平面GMN//平面ABFE。又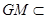 平面GMN,
平面GMN,所以GM//平面ABFE。-----------------------------------------12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
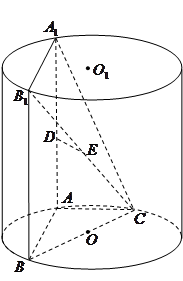
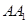 、
、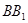 为圆柱
为圆柱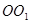 的母线,
的母线,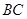 是底面圆
是底面圆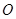 的直径,
的直径,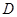 、
、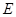 分别是
分别是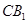 的中点,
的中点,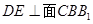 .
.
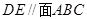 ;
;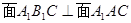 ;
;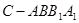 与圆柱
与圆柱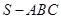 中,侧面
中,侧面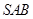 与侧面
与侧面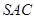 均为等边三角形,
均为等边三角形,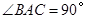 ,
,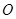 为
为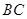 中点.
中点.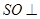 平面
平面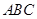 ;
; 的余弦值.
的余弦值.
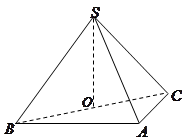
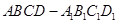 ,
, 是底
是底 对角线的交点.
对角线的交点.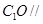 面
面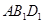 ;
;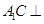 面
面
 中,
中,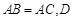 为
为 的中点,
的中点,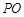 平面
平面 ,垂足
,垂足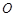 落在线段
落在线段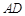 上,已知
上,已知
 ;
;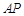 上是否存在点
上是否存在点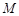 ,使得二面角
,使得二面角 为直二面角?若存在,求出
为直二面角?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 
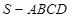 的底面是矩形,
的底面是矩形,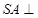 底面
底面 ,
,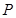 为
为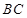 边的中点,
边的中点,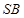 与平面
与平面 所成的角为
所成的角为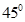 ,且
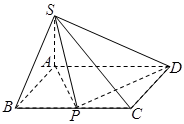
,且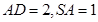 。
。
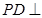 平面
平面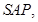
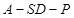 的大小的正切值.
的大小的正切值.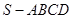 的底面边长为
的底面边长为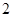 ,高为
,高为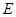 是边
是边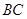 的中点,动点
的中点,动点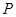 在这个棱锥表面上运动,并且总保持
在这个棱锥表面上运动,并且总保持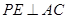 ,则动点
,则动点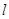 、
、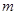 与平面
与平面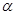 、
、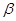 的命题中,正确的是 ( )
的命题中,正确的是 ( )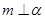 ,
,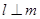 ,则
,则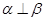 ,
,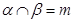 ,
,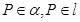 ,且
,且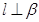
 ,
,
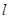 、
、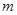 与平面
与平面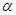 、
、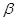 的命题中,正确的是 ( )
的命题中,正确的是 ( )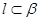 且
且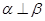 ,则
,则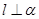 ,
, 且
且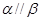 ,则
,则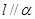 ,
,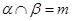 且
且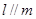 ,则
,则