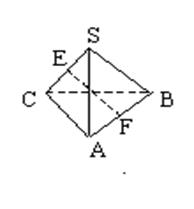
题目内容
如图,在三棱锥 中,侧面
中,侧面 与侧面
与侧面 均为等边三角形,
均为等边三角形,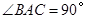 ,
, 为
为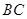 中点.
中点.
(Ⅰ)证明: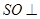 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
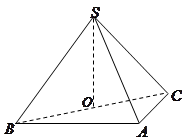
 中,侧面
中,侧面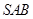 与侧面
与侧面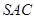 均为等边三角形,
均为等边三角形,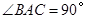 ,
,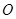 为
为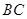 中点.
中点.(Ⅰ)证明:
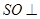 平面
平面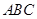 ;
;(Ⅱ)求二面角
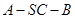 的余弦值.
的余弦值.
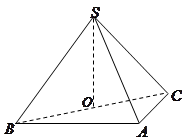
(Ⅰ)见解析;(Ⅱ)二面角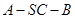 的余弦值为
的余弦值为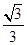 .
.
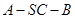 的余弦值为
的余弦值为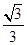 .
. (I)由于侧面SBC为等边三角形,O为BC的中点,所以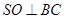 ,
,
只需再取AC的中点M,连接SM,则根据条件易证: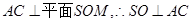 ,
,
问题得证.
(II)解决本小题的关键是找出二面角的平面角,具体做法是取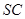 中点
中点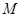 ,连结
,连结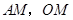 ,由(Ⅰ)知
,由(Ⅰ)知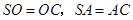 ,
,
得 .
.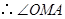 为二面角
为二面角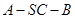 的平面角.
的平面角.
(Ⅰ)由题设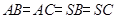
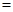
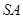 ,连结
,连结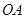 ,
,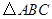 为等腰直角三角形,
为等腰直角三角形,
所以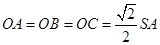 ,且
,且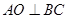 ,又
,又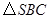 为等腰三角形,
为等腰三角形,
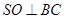 ,且
,且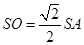 ,从而
,从而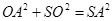 .
.
所以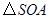 为直角三角形,
为直角三角形,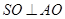 .
.
又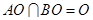 . 所以
. 所以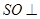 平面
平面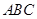 .…………………6分
.…………………6分
(Ⅱ)解法一:取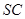 中点
中点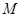 ,连结
,连结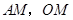 ,由(Ⅰ)知
,由(Ⅰ)知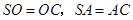 ,
,
得 .
.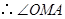 为二面角
为二面角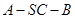 的平面角.
的平面角.
由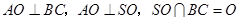 得
得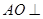 平面
平面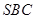 .
.
所以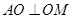 ,又
,又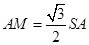 ,
,
故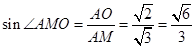 .
.
所以二面角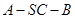 的余弦值为
的余弦值为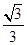 ………………13分
………………13分
解法二:以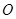 为坐标原点,射线
为坐标原点,射线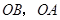 分别为
分别为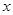 轴、
轴、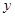 轴的正半轴,建立如图的空间直角坐标系
轴的正半轴,建立如图的空间直角坐标系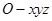 .
.

设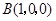 ,则
,则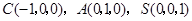 .
.
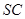 的中点
的中点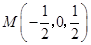 ,
,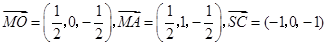 .
.
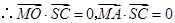 .
.
故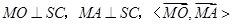 等于二面角
等于二面角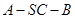 的平面角.……10分
的平面角.……10分
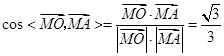 ,
,
所以二面角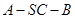 的余弦值为
的余弦值为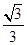 .………12分
.………12分
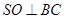 ,
,只需再取AC的中点M,连接SM,则根据条件易证:
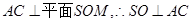 ,
,问题得证.
(II)解决本小题的关键是找出二面角的平面角,具体做法是取
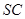 中点
中点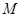 ,连结
,连结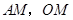 ,由(Ⅰ)知
,由(Ⅰ)知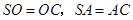 ,
,得
 .
.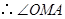 为二面角
为二面角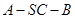 的平面角.
的平面角.(Ⅰ)由题设
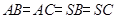
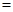
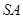 ,连结
,连结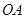 ,
,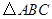 为等腰直角三角形,
为等腰直角三角形,所以
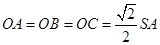 ,且
,且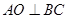 ,又
,又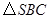 为等腰三角形,
为等腰三角形,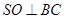 ,且
,且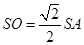 ,从而
,从而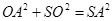 .
. 所以
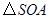 为直角三角形,
为直角三角形,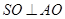 .
.又
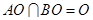 . 所以
. 所以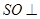 平面
平面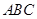 .…………………6分
.…………………6分(Ⅱ)解法一:取
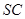 中点
中点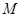 ,连结
,连结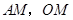 ,由(Ⅰ)知
,由(Ⅰ)知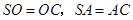 ,
,得
 .
.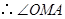 为二面角
为二面角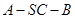 的平面角.
的平面角.由
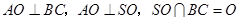 得
得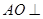 平面
平面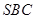 .
.所以
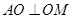 ,又
,又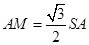 ,
,故
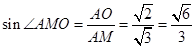 .
.所以二面角
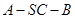 的余弦值为
的余弦值为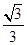 ………………13分
………………13分解法二:以
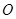 为坐标原点,射线
为坐标原点,射线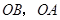 分别为
分别为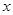 轴、
轴、 轴的正半轴,建立如图的空间直角坐标系
轴的正半轴,建立如图的空间直角坐标系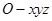 .
.
设
 ,则
,则 .
.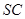 的中点
的中点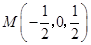 ,
,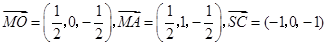 .
.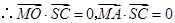 .
.故
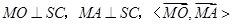 等于二面角
等于二面角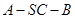 的平面角.……10分
的平面角.……10分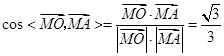 ,
,所以二面角
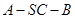 的余弦值为
的余弦值为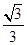 .………12分
.………12分
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 BE,AB
BE,AB
 表示三棱锥B-ACE 的体积,求
表示三棱锥B-ACE 的体积,求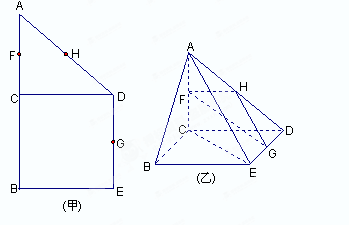
 中,侧棱
中,侧棱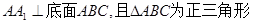 ,点
,点 是
是 的中点,
的中点,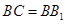 .
.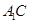 ∥平面
∥平面 ;
;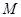 为棱
为棱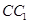 的中点,试证明:
的中点,试证明: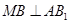 .
.
 ,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE
,EF∥AB,FG∥BC,EG∥AC. AB="2EF." 若M是线段AD的中点。求证:GM∥平面ABFE 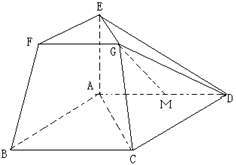

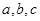 以及平面
以及平面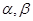 ,给出下列命题:
,给出下列命题: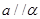 ,
,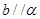 ,则
,则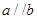
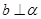 ,则
,则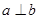
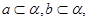 且
且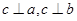 ,则
,则
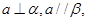 则
则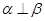
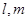 和平面
和平面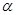 , 则下列命题正确的是
, 则下列命题正确的是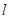 ∥
∥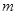 ,
,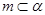 ,则
,则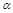 、
、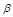 为两个不同的平面,
为两个不同的平面,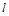 、
、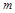 、
、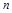 为三条互不相同的直线,
为三条互不相同的直线,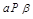 ,
,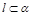 ,则
,则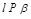 ;
;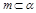 ,
,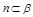 ,
,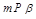 ,
,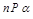 ,则
,则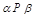 ;
;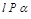 ,
,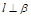 ,则
,则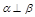 ;
;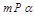 ,
,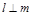 ,
,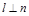 ,则
,则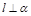 .
.