题目内容
【题目】某高校为增加应届毕业生就业机会,每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估,已知某年度参与评估的毕业生共有2000名,其评估成绩![]() 近似的服从正态分布
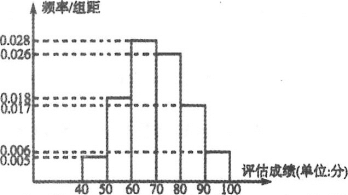
近似的服从正态分布![]() .现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了频率分布直方图:
.现随机抽取了100名毕业生的评估成绩作为样本,并把样本数据进行了分组,绘制了频率分布直方图:
(1)求样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)若学校规定评估成绩超过![]() 分的毕业生可参加
分的毕业生可参加![]() 三家公司的面试.
三家公司的面试.
(ⅰ)用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
,请利用估计值判断这2000名毕业生中,能够参加三家公司面试的人数;
(ⅱ)若三家公司每家都提供甲、乙、丙三个岗位,岗位工资表如下:
公司 | 甲岗位 | 乙岗位 | 丙岗位 |
| 9600 | 6400 | 5200 |
| 9800 | 7200 | 5400 |
| 10000 | 6000 | 5000 |
李华同学取得了三个公司的面试机会,经过评估,李华在三个公司甲、乙、丙三个岗位的面试成功的概率均为![]() ,李华准备依次从
,李华准备依次从![]() 三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会.李华在某公司选岗时,若以该岗位工资与未进行面试公司的工资期望作为抉择依据,问李华可以选择
三家公司进行面试选岗,公司规定:面试成功必须当场选岗,且只有一次机会.李华在某公司选岗时,若以该岗位工资与未进行面试公司的工资期望作为抉择依据,问李华可以选择![]() 公司的哪些岗位?
公司的哪些岗位?
并说明理由.
附:![]() ,若随机变量
,若随机变量![]() ,
,
则![]() .
.
【答案】(1)70,161;(2)(ⅰ)317人;(ⅱ)李华可以选择![]() 公司的甲岗位,
公司的甲岗位,![]() 公司的甲、乙岗位,
公司的甲、乙岗位,![]() 公司的三个岗位.
公司的三个岗位.
【解析】
(1)由样本平均数定义直接计算即可得到平均数,由样本方差公式直接计算即可得到样本方差,问题得解。
(2)(ⅰ)利用正态分布的对称性直接求解。
(ⅱ)利用表中数据求得B公司的工资期望为7260(元),C公司的工资期望为6800(元),由表中数据即可抉择。
(1)由所得数据绘制的频率直方图,得:
样本平均数![]() =45×0.05+55×0.18+65×0.28+75×0.26+85×0.17+95×0.06=70;
=45×0.05+55×0.18+65×0.28+75×0.26+85×0.17+95×0.06=70;
样本方差s2=(45-70)2×0.05+(55-70)2×0.18+(65-70)2×0.28+(75-70)2×0.26+(85-70)2×0.17+(95-70)2×0.06=161;
(2)(i)由(1)可知,![]() ,
,![]() ,故评估成绩Z服从正态分布N(70,161),
,故评估成绩Z服从正态分布N(70,161),
所以![]() .
.
在这2000名毕业生中,能参加三家公司面试的估计有2000×0.1587≈317人.
(ii)李华可以选择A公司的甲岗位,B公司的甲、乙岗位,C公司的三个岗位.
理由如下:
设B、C公司提供的工资为XB,XC,则XB,XC都为随机变量,其分布列为
公司 | 甲岗位 | 乙岗位 | 丙岗位 |
XB | 9800 | 7200 | 5400 |
XC | 10000 | 6000 | 5000 |
P | 0.3 | 0.3 | 0.4 |
则B公司的工资期望:E(XB)=9800×0.3+7200×0.3+5400×0.4=7260(元),
C公司的工资期望:E(XC)=10000×0.3+6000×0.3+5000×0.4=6800(元),
因为A公司的甲岗位工资9600元大于B、C公司的工资期望,乙岗位工资6400元小于B、C公司的工资期望,故李华先去A公司面试,若A公司给予甲岗位就接受,否则去B公司;B公司甲、乙岗位工资都高于C公司的工资期望,故B公司提供甲、乙岗位就接受,否则去C公司;在C公司可以依次接受甲、乙、丙三种岗位中的一种岗位.

【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶7元,未售出的酸奶降价处理,以每瓶1.5元的价格当天全部处理完.据往年销售经验,每天需求量与当天最高气温(单位:![]() )有关,如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关,如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得到下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 14 | 34 | 27 | 9 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),若该超市在六月份每天的进货量均为450瓶,写出
(单位:元),若该超市在六月份每天的进货量均为450瓶,写出![]() 的所有可能值,并估计
的所有可能值,并估计![]() 大于零的概率.
大于零的概率.
【题目】某高校在2019的自主招生考试中,考生笔试成绩分布在![]() ,随机抽取200名考生成绩作为样本研究,按照笔试成绩分成5组,得到的如下的频率分布表:
,随机抽取200名考生成绩作为样本研究,按照笔试成绩分成5组,得到的如下的频率分布表:
组号 | 分数区间 | 频数 | 频率 |
1 |
| 70 | 0.35 |
2 |
| 10 | 0.05 |
3 |
| ① | 0.20 |
4 |
| 60 | 0.30 |
5 |
| 20 | ② |
(1)请先求出频率分布表中①、②位置的相应数据,再完成频率分布直方图;
(2)为了能选拨出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组各组抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,从这6名学生中随机抽取2名学生进行外语交流面试,求这2名学生均来自同一组的概率.