题目内容
16. Ⅰ.Fe3+可以与SCN-、CN-、F-、有机分子等形成很多的配合物.请回答下列问题:
Ⅰ.Fe3+可以与SCN-、CN-、F-、有机分子等形成很多的配合物.请回答下列问题:(1)基态Fe3+的电子排布式可表示为1s22s22p63s23p63d5.
(2)与CN-互为等电子体的分子有N2和CO(写出2种).
(3)金属配合物Fe(CO)n的中心原子价电子数与配体提供电子总数之和为18,则n=5.
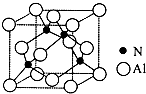
Ⅱ.已知氮化铝的晶胞结构如图所示.请回答下列问题:
(4)下列说法正确的是BC(填序号).
A.氮化铝晶胞结构与NaCl相同 B.第一电离能 N>Al
C.电负性N>Al D.原子半径 N>Al
(5)NH3空间构型为三角锥形;已知(CH3)3Al为非极性分子,则其中铝原子的杂化方式为sp2.
(6)若氮化铝可由(CH3)3Al和NH3在一定条件下反应制得,则反应的方程式为(CH3)3Al+NH3$\frac{\underline{\;一定条件\;}}{\;}$AlN+3CH4 .
(7)若Al与N 原子最近的距离为a cm,则该晶体的密度为$\frac{41×3\sqrt{3}}{16{a}^{3}{N}_{A}}$ g/cm3.(阿伏加德罗常数用NA表示)
分析 (1)原子形成阳离子失去高能层中该能级电子,再失去同能层中低能级电子,然后再失去低能层中电子;
(2)原子总数相等、价电子总数相等的微粒互为等电子体;
(3)Fe是26元素,其价电子数是8,每个配体CO分子提供电子数为2;
(4)A.NaCl晶胞中,没有氯离子周围有6个钠离子,每个钠离子周围有6个氯离子;
B.元素非金属性越强,原子越不易失去电子,第一电离能越大;
C.非金属性越强,电负性越大;
D.同周期自左而右原子半径减小、同主族自上而下原子半径增大;
(5)氨气分子为三角锥形;(CH3)3Al为非极性分子,Al原子与3个甲基形成平面正三角形结构;
(6)晶胞中晶胞中N原子数目为4、Al原子数目为8×$\frac{1}{8}$+6×$\frac{1}{2}$=4,氮化铝化学式为AlN,可由(CH3)3Al和NH3在一定条件下反应制得,由元素守恒可知还生成甲烷;
(7)顶点白色与相邻的黑色球位于晶胞体对角线上,黑色球到侧面距离均相等,过晶胞中左侧2个黑色球、右侧2个黑色球及面心白色球作左、右侧面的平行面,可以将体对角线4等份,即顶点白色球与相邻黑色球距离为晶胞体对角线的$\frac{1}{4}$,据此计算晶胞棱长,进而计算晶胞体积.利用均摊法计算晶胞中Al、N原子数目,进而计算晶胞质量,再根据ρ=$\frac{m}{ρ}$计算晶胞密度.
解答 解:(1)Fe原子核外电子排布为1s22s22p63s23p63d64s2,原子形成阳离子失去高能层中该能级电子,再失去同能层中低能级电子,然后再失去低能层中电子,故基态Fe3+的电子排布式可表示为1s22s22p63s23p63d5,
故答案为:1s22s22p63s23p63d5;
(2)原子总数相等、价电子总数相等的微粒互为等电子体,与CN-互为等电子体的分子有N2和CO,
故答案为:N2和CO;
(3)Fe是26元素,其价电子数是8,每个配体CO分子提供电子数为2,则8+2n=18,故n=5,
故答案为:5;
(4)A.NaCl晶胞中,没有氯离子周围有6个钠离子,每个钠离子周围有6个氯离子,AlN晶体中每个N原子周围有3个Al原子,二者晶胞结构不相同,故A错误;
B.元素非金属性越强,原子越不易失去电子,第一电离能越大,故第一电离能 N>Al,故B正确;
C.非金属性越强,电负性越大,故电负性N>Al,故C正确;
D.同周期自左而右原子半径减小、同主族自上而下原子半径增大,故原子半径 N<Al,故D错误,
故选:BC;
(5)氨气分子为三角锥形;(CH3)3Al为非极性分子,Al原子与3个甲基形成平面正三角形结构,Al原子采取sp2杂化,
故答案为:三角锥形;sp2;
(6)晶胞中晶胞中N原子数目为4、Al原子数目为8×$\frac{1}{8}$+6×$\frac{1}{2}$=4,氮化铝化学式为AlN,可由(CH3)3Al和NH3在一定条件下反应制得,由元素守恒可知还生成甲烷,反应方程式为:(CH3)3Al+NH3$\frac{\underline{\;一定条件\;}}{\;}$AlN+3CH4 ,
故答案为:(CH3)3Al+NH3$\frac{\underline{\;一定条件\;}}{\;}$AlN+3CH4 ;
(7)顶点白色与相邻的黑色球位于晶胞体对角线上,黑色球到侧面距离均相等,过晶胞中左侧2个黑色球、右侧2个黑色球及面心白色球作左、右侧面的平行面,可以将体对角线4等份,即顶点白色球与相邻黑色球距离为晶胞体对角线的$\frac{1}{4}$,则晶胞体对角线长为4a cm,晶胞棱长为$\frac{4\sqrt{3}a}{3}$ cm,晶胞中N原子数目为4、Al原子数目为8×$\frac{1}{8}$+6×$\frac{1}{2}$=4,故晶胞质量为4×$\frac{41}{{N}_{A}}$g,则晶胞密度为4×$\frac{41}{{N}_{A}}$g÷($\frac{4\sqrt{3}a}{3}$ cm)3=$\frac{41×3\sqrt{3}}{16{a}^{3}{N}_{A}}$g.cm-3,
故答案为:$\frac{41×3\sqrt{3}}{16{a}^{3}{N}_{A}}$.
点评 本题是对物质结构的考查,涉及核外电子排布、等电子体、配合物、电负性、电离能、微粒大小比较、分子构型、杂化方式、晶胞计算等,(7)中计算为易错点、难点,需要学生具备一定的空间想象与数学计算能力,难度中等.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案| A. | 丙氨酸与苯丙氨酸脱水,最多可以生成3种二肽 | |
| B. | 对苯二甲酸(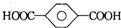 )与乙二醇(HOCH2CH2OH)能通过加聚反应制取聚酯纤维 )与乙二醇(HOCH2CH2OH)能通过加聚反应制取聚酯纤维(  ) ) | |
| C. | 迷迭香酸的结构为 它可以发生酯化、水解、加成、取代、氧化等反应 它可以发生酯化、水解、加成、取代、氧化等反应 | |
| D. | 分子式为C5H12O的醇,能在铜催化下被O2氧化为醛的同分异构体有5种 |
| 族 周期 | IA | IIA | IIIA | IVA | VA | VIA | VIIA | 0 |
| 2 | ⑤ | ⑥ | ⑦ | ⑧ | ||||
| 3 | ① | ③ | ④ | ⑨ | ||||
| 4 | ② |
(1)在上述元素中,金属性最强的是K,在③~⑦元素中,原子半径最大的是Mg;
(2)①~⑨中元素最高价氧化物对应的水化物中酸性最强的是HClO4(填物质化学式).
写出①和④的最高价氧化物对应的水化物反应的离子方程式Al(OH)3+OH-═AlO2-+2H2O.
(3)用电子式表示③和⑨形成的化合物的形成过程
 .
.(4)表中元素①和⑦可以形成一种淡黄色物质X,写出X的电子式:
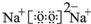 ,该物质所含化学键类型离子键、共价键,0.1mol X与水反应转移电子数为:0.1NA
,该物质所含化学键类型离子键、共价键,0.1mol X与水反应转移电子数为:0.1NA(5)表中元素⑥和⑧可形成一种相对分子量为66的共价化合物Y,Y分子中各原子均达到“8电子稳定结构”,Y的结构式F-N=N-F.
| A. | 羟基与氢氧根有相同的化学式和电子式 | |
| B. | 乙醇的官能团是-OH,乙醇是含-OH的化合物 | |
| C. | 常温下,1mol乙醇可与足量的Na反应生成11.2LH2 | |
| D. | 由工业酒精获得无水乙醇的方法是直接加热蒸馏 |
| A. | 澄清石灰水 | B. | 氯化钡溶液 | C. | 品红溶液 | D. | 紫色石蕊试液 |
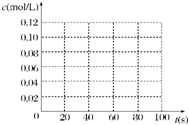 在100℃时,将0.100mol 的四氧化二氮气体充入 1L 恒容真空的密闭容器中,隔一段时间对该容器内的物质浓度进行分析得到下表数据:
在100℃时,将0.100mol 的四氧化二氮气体充入 1L 恒容真空的密闭容器中,隔一段时间对该容器内的物质浓度进行分析得到下表数据:| 时间(s) | 0 | 20 | 40 | 60 | 80 |
| c(N2O4)(mol/L) | 0.100 | c1 | 0.050 | c3 | c4 |
| c(NO2)(mol/L) | 0.000 | 0.060 | c2 | 0.120 | 0.120 |
从表中分析:c1<c2;c3=c4(填“>”、“<”或“=”).
(2)在下图中画出并标明此反应中c(N2O4)和c(NO2)的浓度随时间变化的曲线.
(3)在上述条件下,从反应开始直至达到化学平衡时,四氧化二氮的平均反应速率为0.001mol/(L•s).
(4)反应达到平衡后,下列条件的改变可使NO2气体的浓度增大的是B
A.增大容器的容积 B.再充入一定量的N2O4
C.分离出一定量的NO2 D.再充入一定量的He.
| A. | 牛肉 | B. | 芹菜 | C. | 鸡蛋 | D. | 牛奶 |
