题目内容
1.能将Al2(SO4)3、(NH4)2SO4、KCl、MgCl2、FeCl2、Fe2(SO4)3六种溶液鉴别出来的一种试剂是( )| A. | NaOH溶液 | B. | KSCN溶液 | C. | AgNO3溶液 | D. | BaCl2溶液 |
分析 Al2(SO4)3、(NH4)2SO4、KCl、MgCl2、FeCl2、Fe2(SO4)3六种溶液分别与NaOH溶液混合的现象为:先生成白色沉淀后沉淀溶解、刺激性气体、无现象、白色沉淀、显生成白色沉淀迅速变为灰绿色最后为红褐色、红褐色沉淀,以此来解答.
解答 解:A.Al2(SO4)3、(NH4)2SO4、KCl、MgCl2、FeCl2、Fe2(SO4)3六种溶液分别与NaOH溶液混合的现象为:先生成白色沉淀后沉淀溶解、刺激性气体、无现象、白色沉淀、显生成白色沉淀迅速变为灰绿色最后为红褐色、红褐色沉淀,现象不同,可鉴别,故A正确;
B.KSVN溶液只能鉴别Fe2(SO4)3,故B错误;
C.均与硝酸银反应生成白色沉淀,不能鉴别,故C错误;
D.Al2(SO4)3、(NH4)2SO4、Fe2(SO4)3均与氯化钡反应生成白色沉淀,不能鉴别,故D错误;
故选A.
点评 本题考查物质的鉴别,为高频考点,把握发生的反应及反应中的不同现象为解答的关键,侧重分析与实验能力的考查,注意现象相同不能鉴别物质,题目难度不大.

练习册系列答案
相关题目
9.水的电离平衡曲线如图所示,下列说法中不正确的是( )
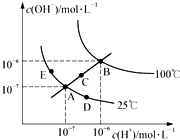

| A. | 图中五点的KW间的关系为:B>C>A=D=E | |
| B. | 若从A点到D点,可采用:恒温条件下,在水中加入少量的醋酸,提高溶液酸性 | |
| C. | 若从A点到C点,可采用:恒温条件下,在水中加入少量的醋酸铵,促进水的电离 | |
| D. | 100℃时,将pH=2的硫酸与0.01mol•L-1的KOH溶液等体积混合后,溶液中c(H+)=c(OH-)=10-6mol•L-1 |
6. 在10L恒容密闭容器中充入X(g)和Y(g),发生反应X(g)+Y(g)?M(g)+N(g)所得实验数据如表:
在10L恒容密闭容器中充入X(g)和Y(g),发生反应X(g)+Y(g)?M(g)+N(g)所得实验数据如表:
回答下列问题:
(1)实验①中,若5min时测得,n(M)=0.050mo1,则0至5min时间内,用N表示的平均反应速率为1.0×10-3mol/(L•min).
(2)实验③平衡常数为1.0,该正反应为放热反应(填“吸热”或“放热”)
(3)能说明上述反应一定达到平衡的条件是C.
A.c(Y)=c(N) B.平均分子量不再变化
C.v正(X)=v逆(M) D.温度和压强一定时,混合气体的密度不再变化
(4)实验③中,达到平衡时,X的转化率为60%多余.
(5)实验③、④中,达到平衡时,a与b的关系为A(填选项),请解释原因若温度不变,则b=$\frac{1}{2}$a,该反应为放热反应,温度升高,平衡向逆反应方向移动,故b<$\frac{1}{2}$a,即a>2b.
A.a>2b B.a=2b C.b<a<2b D.a<b
(6)如图是实验①中c(M)随时间变化的曲线图,请在图中画出实验②中c(M)随时间变化的曲线图.
 在10L恒容密闭容器中充入X(g)和Y(g),发生反应X(g)+Y(g)?M(g)+N(g)所得实验数据如表:
在10L恒容密闭容器中充入X(g)和Y(g),发生反应X(g)+Y(g)?M(g)+N(g)所得实验数据如表:| 实验编号 | 温度/℃ | 起始时物质的量/mol | 平衡时物质的量/mol | |
| n(X) | n(Y) | n(M) | ||
| ① | 700 | 0.40 | 0.10 | 0.090 |
| ② | 800 | 0.10 | 0.40 | 0.080 |
| ③ | 800 | 0.20 | 0.30 | a |
| ④ | 900 | 0.10 | 0.15 | b |
(1)实验①中,若5min时测得,n(M)=0.050mo1,则0至5min时间内,用N表示的平均反应速率为1.0×10-3mol/(L•min).
(2)实验③平衡常数为1.0,该正反应为放热反应(填“吸热”或“放热”)
(3)能说明上述反应一定达到平衡的条件是C.
A.c(Y)=c(N) B.平均分子量不再变化
C.v正(X)=v逆(M) D.温度和压强一定时,混合气体的密度不再变化
(4)实验③中,达到平衡时,X的转化率为60%多余.
(5)实验③、④中,达到平衡时,a与b的关系为A(填选项),请解释原因若温度不变,则b=$\frac{1}{2}$a,该反应为放热反应,温度升高,平衡向逆反应方向移动,故b<$\frac{1}{2}$a,即a>2b.
A.a>2b B.a=2b C.b<a<2b D.a<b
(6)如图是实验①中c(M)随时间变化的曲线图,请在图中画出实验②中c(M)随时间变化的曲线图.
13.一定温度下,某饱和碳酸钠溶液中碳酸钠的质量分数为ω%,加入a g无水碳酸钠可析出bg碳酸钠晶体(Na2CO3•10H2O),则原溶液中溶质质量减少( )
| A. | (b-a)g | B. | (b-a)×ωg | C. | ($\frac{53b}{143}$-a)g | D. | ($\frac{53b}{143}$-a)×ω%g |
 恒温恒容时,NO2和N2O4之间发生反应N2O4(g)?2NO2(g),如图所示.
恒温恒容时,NO2和N2O4之间发生反应N2O4(g)?2NO2(g),如图所示.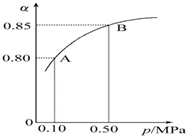 面对全球近期的气候异常,环境问题再次成为焦点.化工厂以及汽车尾气排放的二氧化硫、一氧化碳、氮氧化物(NOx)等气体已成为大气污染的主要因素.
面对全球近期的气候异常,环境问题再次成为焦点.化工厂以及汽车尾气排放的二氧化硫、一氧化碳、氮氧化物(NOx)等气体已成为大气污染的主要因素.