题目内容
5.t℃时Na2SO4的溶解度是S g,其饱和溶液密度d g•cm-3,物质的量浓度为c mol•L-1.向足量饱和溶液中,加入X g无水Na2SO4或蒸发Yg水后恢复t℃,均能获得W g芒硝晶体,下列关系式正确的是( )| A. | c=$\frac{dS}{142(S+100)}$ mol•L-1 | B. | S=$\frac{142W}{180W+322Y}$g | ||
| C. | X=YS | D. | W=$\frac{3220X}{1420-18S}$g |
分析 A.根据c=$\frac{1000ρω}{M}$计算,根据溶解度计算饱和溶液的质量分数;
B.饱和溶液蒸发掉Yg水恢复到t℃时,获得Wg Na2SO4•10H2O晶体,故Wg晶体再加入(蒸发掉的)Y g水时,Wg芒硝晶体就可恰好溶解恢复到原饱和溶液,即Y g水与Wg Na2SO4•10H2O构成饱和溶液,据此计算;
C.向足量饱和溶液中加入X g无水Na2SO4或蒸发掉Y g水后恢复t℃,均能获得W g芒硝晶体,由于硫酸钠能与水反应而使饱和硫酸钠溶液因减少水而析出晶体,因此可判断加入X g无水Na2SO4•相当于蒸发掉Y g水,即蒸发的Y g水中溶解有X g的硫酸钠;
D.析出的芒硝晶体质量等于加入Xg硫酸钠质量与饱和溶液减少的质量,根据化学式计算硫酸钠、结晶水的质量,进而计算结晶水溶解硫酸钠的质量,结合溶解度S计算.
解答 解:A.t℃时Na2SO4的溶解度是S g,则饱和溶液的质量分数为:$\frac{Sg}{100g+Sg}$=$\frac{S}{100+S}$,根据c=$\frac{1000ρω}{M}$可知该溶液物质的量浓度=$\frac{1000×ρ×\frac{S}{100+S}}{142}$mol/L=$\frac{1000dS}{142(100+S)}$mol•L-1,故A错误;
B.饱和溶液蒸发掉Yg水恢复到t℃时,获得Wg Na2SO4•10H2O晶体,逆向思维即再加入(蒸发掉的)Y g水时,Wg芒硝晶体就可恰好溶解恢复到原饱和溶液,即Y g水与Wg Na2SO4•10H2O构成饱和溶液,饱和溶液中溶质质量=Wg×$\frac{142}{322}$,溶液的质量=Y+W,此时硫酸钠的溶解度S=$\frac{\frac{142}{322}×Wg}{Yg+Wg-\frac{142}{322}×Wg}$×100g=$\frac{14200W}{180W+322Y}$g,故B错误;
C.加入X g无水硫酸钠或蒸发掉Y g水后恢复到t℃,均能获得W g芒硝晶体说明Y g水后中溶解X g无水硫酸钠恰好形成饱和溶液,此时硫酸钠的溶解度S=$\frac{Xg}{Yg}$×100g,则X=$\frac{YS}{100}$,故C错误;
D.加入X g的无水硫酸钠与饱和溶液中的水反应而使饱和溶液因水减少而析出晶体,W g硫酸钠晶体中所含结晶水质量=W g×$\frac{180}{322}$,所含硫酸钠的质量=W g×$\frac{142}{322}$,而其中(W g×$\frac{142}{322}$-X)g硫酸钠完全溶解于W g×$\frac{180}{322}$g水恰好成为饱和溶液,则$\frac{S}{100}$=$\frac{Wg×\frac{142}{322}-Xg}{\frac{180}{322}×Wg}$,则析出晶体质量W=$\frac{3220X}{1420-18S}$g,故D正确;
故选D.
点评 本题考查溶液浓度有关计算,涉及质量分数、溶解度、物质的量浓度,属于字母型计算,题目难度较大,试题已知条件甚多,要求学生综合分析利用,试题充分考查了学生的分析、理解能力及灵活应用基础知识的能力.

| A. | 16 g | B. | 32 g | C. | 16 | D. | 32 |
| A. | 甲苯 | B. | 金属Cu | C. | NaCl溶液 | D. | HCl溶液 |
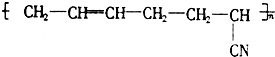 丁腈橡胶具有优良的耐油、耐高温性能,合成丁腈橡胶的原料是( )
丁腈橡胶具有优良的耐油、耐高温性能,合成丁腈橡胶的原料是( )①CH2=CH-CH=CH2 ②CH3-C≡C-CH3 ③CH2=CH-CN
④
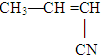 ⑤CH3-CH═CH2 ⑥CH3-CH=CH-CH3.
⑤CH3-CH═CH2 ⑥CH3-CH=CH-CH3.| A. | ③⑥ | B. | ②③ | C. | ①③ | D. | ④⑤ |
| A. | 标准状况下,11.2 L的己烷所含的分子数为0.5 NA 个 | |
| B. | 28 g乙烯所含共用电子对数目为6 NA个 | |
| C. | 标准状况下,11.2 L二氯甲烷所含分子数为0.5 NA个 | |
| D. | 现有乙烯、丙烯、丁烯的混合气体共14 g,其原子数为6 NA个 |
| A. | 该分子是氧元素的一种同位素 | B. | 该分子的摩尔质量为64 g | ||
| C. | 该物质与氧气互为同素异形体 | D. | 该物质是一种氧化物 |
| A. | 2.26 t | B. | 1.98 t | C. | 1.65 t | D. | 1.06 t |
 ;
;