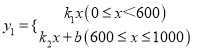【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
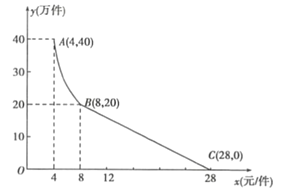
【题目】某食品厂生产一种半成品食材,产量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足函数关系式
满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材的市场需求量
,从市场反馈的信息发现,该半成品食材的市场需求量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足一次函数关系,如下表:
满足一次函数关系,如下表:
销售价格 | 2 | 4 |
| 10 |
市场需求量 | 12 | 10 |
| 4 |
已知按物价部门规定销售价格x不低于2元![]() 千克且不高于10元
千克且不高于10元![]() 千克
千克
![]() 求q与x的函数关系式;
求q与x的函数关系式;
![]() 当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
![]() 当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃
当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃![]() 若该半成品食材的成本是2元
若该半成品食材的成本是2元![]() 千克.
千克.
![]() 求厂家获得的利润
求厂家获得的利润![]() 百元
百元![]() 与销售价格x的函数关系式;
与销售价格x的函数关系式;
![]() 当厂家获得的利润
当厂家获得的利润![]() 百元
百元![]() 随销售价格x的上涨而增加时,直接写出x的取值范围
随销售价格x的上涨而增加时,直接写出x的取值范围![]() 利润
利润![]() 售价
售价![]() 成本
成本![]()
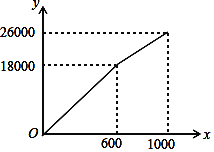
【题目】某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量y(台)与销售单价x(元)的关系可以近似地看做一次函数,如下表所示:
x | 22 | 24 | 26 | 28 |
y | 90 | 80 | 70 | 60 |
(1)请直接写出y与x之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为ω(元),求ω与x之间的函数关系式,当x取何值时,ω的值最大?最大值是多少?
【题目】某种植基地种植一种蔬菜,它的成本是每千克2元,售价是每千克3元,年销量为10万千克.基地准备拿出一定的资金作绿色开发,若每年绿色开发投入的资金为![]() (万元),该种蔬菜的年销量将是原年销量的
(万元),该种蔬菜的年销量将是原年销量的![]() 倍,
倍,![]() 与
与![]() 的关系如下表:
的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 1 | 1.5 | 1.8 | 1.9 | 1.8 | 1.5 | … |
(1)猜想![]() 与
与![]() 之间的函数类型是________函数,求出该函数的表达式并验证;
之间的函数类型是________函数,求出该函数的表达式并验证;
(2)求年利润![]() (万元)与绿色开发投入的资金
(万元)与绿色开发投入的资金![]() (万元)之间的函数关系式,当绿色开发投入的资金不低于3万元,又不超过5万元时,求此时年利润
(万元)之间的函数关系式,当绿色开发投入的资金不低于3万元,又不超过5万元时,求此时年利润![]() (万元)的最大值;
(万元)的最大值;
(注:年利润![]() 销售总额-成本费-绿色开发投入的资金)
销售总额-成本费-绿色开发投入的资金)
(3)若提高种植人员的奖金,发现又增加一部分年销量,经调查发现:再次增加的年销量![]() (万千克)与每年提高种植人员的奖金
(万千克)与每年提高种植人员的奖金![]() (万元)之间满足
(万元)之间满足![]() ,若基地将投入5万元用于绿色开发和提高种植人员的奖金,应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入?(
,若基地将投入5万元用于绿色开发和提高种植人员的奖金,应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入?(![]() )
)