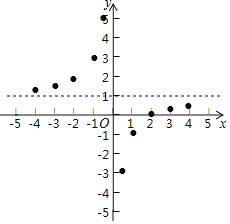【题目】为了抗击新冠病毒疫情,全国人民众志成城,守望相助.春节后某地一水果购销商安排15辆汽车装运A,B,C三种水果120吨销售,所得利润全部捐赠湖北抗疫.已知按计划15辆汽车都要装满且每辆汽车只能装同一种水果,每种水果所用车辆均不少于3辆,汽车对不同水果的运载量和每吨水果销售获利情况如下表.
水果品种 | A | B | C |
汽车运载量(吨/辆) | 10 | 8 | 6 |
水果获利(元/吨) | 800 | 1200 | 1000 |
(1)设装运A种水果的车辆数为x辆,装运B种水果车辆数为y辆,根据上表提供的信
息,
①求y与x之间的函数关系式;
②设计车辆的安排方案,并写出每种安排方案;
(2)若原有获利不变的情况下,当地政府按每吨50元的标准实行运费补贴,该经销商打算将获利连同补贴全部捐出.问应采用哪种车辆安排方案,可以使这次捐款数w(元)最大化?捐款w(元)最大是多少?
【题目】参照学习函数的过程与方法,探究函数y=![]() 的图象与性质.
的图象与性质.
因为y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我们对比函数y=﹣
+1,所以我们对比函数y=﹣![]() 来探究.
来探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y=![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y=![]() 的图象是由y=﹣
的图象是由y=﹣![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设A(x1,y1),B(x2,y2)是函数y=![]() 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
的图象上的两点,且x1+x2=0,试求y1+y2+3的值.