ЬтФПФкШн
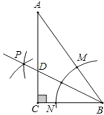
ЁОЬтФПЁПвбжЊЃКдкЁїABCжаЃЌABЃНACЃЌЕуDЮЊBCБпЕФжаЕуЃЌЕуFЪЧABБпЩЯвЛЕуЃЌЕуEдкЯпЖЮDFЕФбгГЄЯпЩЯЃЌЁЯBAEЃНЁЯBDFЃЌЕуMдкЯпЖЮDFЩЯЃЌЁЯABE=ЁЯDBMЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЕБЁЯABCЃН45ЁуЪБЃЌЧѓжЄЃКAEЃН![]() MDЃЛ
MDЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЁЯABCЃН60ЁуЪБЃЌ
ЂйжБНгаДГіЯпЖЮAEЃЌMDжЎМфЕФЪ§СПЙиЯЕЃЛ
ЂкбгГЄBMЕНPЃЌЪЙMPЃНBMЃЌСЌНгCPЃЌШєABЃН7ЃЌAEЃН![]() ЃЌЬНЧѓsinЁЯPCBЕФжЕЃЎ
ЃЌЬНЧѓsinЁЯPCBЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂйAEЃН2DMЃЌРэгЩМћНтЮіЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтжЊЁЯBAEЃНЁЯBDMЃЌЁЯABEЃНЁЯDBMЙЪгаЁїABEЁзЁїDBMЃЌДгЖјЕУЕНAEЃКDMЃНABЃКBDЃЌЖјЁЯABCЃН45ЁуЃЌдйЕУЕНABЃН![]() BDЃЌдђгаAEЃН
BDЃЌдђгаAEЃН![]() MDЃЛ
MDЃЛ
ЃЈ2ЃЉЂйгЩгкЁїABEЁзЁїDBMЃЌЯрЫЦБШЮЊ2ЃЌЙЪгаEBЃН2BMЃЌНјЖјШЗЖЈГіAEгыDMЕФЙиЯЕЃЛ
ЂкгЩЬтвтжЊЕУЁїBEPЮЊЕШБпШ§НЧаЮЃЌгаEMЁЭBPЃЌЁЯBMDЃНЁЯAEBЃН90ЁуЃЌдкRtЁїAEBжаЧѓЕУAEЁЂABЁЂtanЁЯEABЕФжЕЃЌгЩDЮЊBCжаЕуЃЌMЮЊBPжаЕуЃЌЕУDMЁЮPCЃЌЧѓЕУtanЁЯPCBЕФжЕЃЌдкRtЁїABDКЭRtЁїNDCжаЃЌгЩШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓЕУADЁЂNDЕФжЕЃЌНјЖјЧѓЕУtanЁЯPCBЕФжЕЃЎ
ЃЈ1ЃЉжЄУїЃКШчЭМ1ЃЌСЌНгADЃЎ
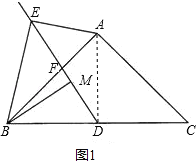
ЁпABЃНACЃЌBDЃНCDЃЌ
ЁрADЁЭBCЃЎ
гжЁпЁЯABCЃН45ЁуЃЌ
ЁрBDЃНABcosЁЯABCЃЌМДABЃН![]() BDЃЎ
BDЃЎ
ЁпЁЯBAEЃНЁЯBDMЃЌЁЯABEЃНЁЯDBMЃЌ
ЁрЁїABEЁзЁїDBMЃЎ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрAEЃН![]() MDЃЎ
MDЃЎ
ЃЈ2ЃЉЂйШчЭМ2ЃЌСЌНгADЃЌEPЃЌЙ§NзїNHЁЭACЃЌДЙзуЮЊHЃЌСЌНгNHЃЌ
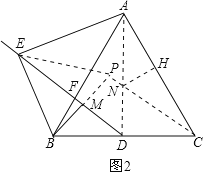
ЁпABЃНACЃЌЁЯABCЃН60ЁуЃЌ
ЁрЁїABCЪЧЕШБпШ§НЧаЮЃЌ
гжЁпDЮЊBCЕФжаЕуЃЌ
ЁрADЁЭBCЃЌЁЯDACЃН30ЁуЃЌBDЃНDCЃН![]() ABЃЌ
ABЃЌ
ЁпЁЯBAEЃНЁЯBDMЃЌЁЯABEЃНЁЯDBMЃЌ
ЁрЁїABEЁзЁїDBMЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН2ЃЌЁЯAEBЃНЁЯDMBЃЌМДAEЃН2DMЃЛ
ЃН2ЃЌЁЯAEBЃНЁЯDMBЃЌМДAEЃН2DMЃЛ
ЂкЁпЁїABEЁзЁїDBMЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН2ЃЌ
ЃН2ЃЌ
ЁрEBЃН2BMЃЌ
гжЁпBMЃНMPЃЌ
ЁрEBЃНBPЃЌ
ЁпЁЯEBMЃНЁЯEBA+ЁЯABMЃНЁЯMBD+ЁЯABMЃНЁЯABCЃН60ЁуЃЌ
ЁрЁїBEPЮЊЕШБпШ§НЧаЮЃЌ
ЁрEMЁЭBPЃЌ
ЁрЁЯBMDЃН90ЁуЃЌ
ЁрЁЯAEBЃН90ЁуЃЌ
дкRtЁїAEBжаЃЌAEЃН2![]() ЃЌABЃН7ЃЌ
ЃЌABЃН7ЃЌ
ЁрBEЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрtanЁЯEABЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпDЮЊBCжаЕуЃЌMЮЊBPжаЕуЃЌ
ЁрDMЁЮPCЃЌ
ЁрЁЯMDBЃНЁЯPCBЃЌ
ЁрЁЯEABЃНЁЯPCBЃЌ
ЁрtanЁЯPCBЃН![]() ЃЎ
ЃЎ