题目内容
【题目】如图,在平面直角坐标系中,长方形ABCD的顶点B在坐标原点,顶点A、C分别在y轴、x轴的负半轴上,其中![]() ,
,![]() ,将矩形ABCD绕点D逆时针旋转得到矩形
,将矩形ABCD绕点D逆时针旋转得到矩形![]() ,点
,点![]() 恰好落在x轴上,线段
恰好落在x轴上,线段![]() 与CD交于点E,那么点E的坐标为
与CD交于点E,那么点E的坐标为![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
连接BD,B'D,根据矩形ABCD绕点D逆时针旋转得到矩形A'B'C'D,可得BD=B'D,再根据DC⊥BB',即可得到BC=B'C=2=A'D,再判定△B'EC≌△DEA',得到B'E=DE,设CE=x,则B'E=DE=4x,根据Rt△B'EC中,![]() ,可得
,可得![]() ,求得x的值即可得到点E的坐标.
,求得x的值即可得到点E的坐标.
如图,
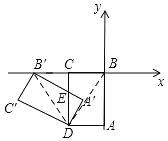
连接BD,B′D,
∵矩形ABCD绕点D逆时针旋转得到矩形A′B′C′D,
∴BD=B′D,
又∵DC⊥BB′,A(0,4),C(2,0),
∴BC=B′C=2=A′D,
又∵∠B′CE=∠DA′E=![]() ,∠B′EC=∠DEA′,
,∠B′EC=∠DEA′,
∴△B′EC≌△DEA′,
∴B′E=DE,
设CE=x,则B′E=DE=4x,
∵Rt△B′EC中![]()
∴![]()
解得x=32,
∴E(2,![]() ),
),
故选:A.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目