题目内容
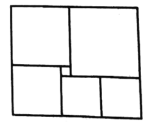
【题目】一个由木条制作的长方形窗户如图所示，里面有6个小正方形，且右下角的正方形的边长比中间最小的正方形的边长多0.4米，若制作这个长方形窗户需要的木条总长至少为a米，则a=________
【答案】
.
【解析】
设右下角的正方形边长为x米，依次得到各个正方形的边长，利用最大的正方形的边长的两种不同表达方式列出方程，求得右下角的正方形的边长，进而求得制作这个长方形窗户需要的木条总长．
解：如图，设正方形A的边长为x米，则
中间最小的正方形的边长为（ x-0.4）米，
正方形B的边长为x米，
正方形C的边长为x+（ x-0.4）=（2x-0.4）米，
正方形D的边长为（ x-0.4）+（2x-0.4）=（3x-0.8）米，
正方形E的边长为 （ x-0.4）+（3x-0.8）=（4x-1.2）米或2x-（ x-0.4）=（x+0.4）米，
由题意得：4x-1.2= x+0.4,
解得x= 
，
∴a=3[x+（x+0.4）]+（2x-0.4）+3[（3x-0.8）+（x+0.4）]+ （ x-0.4）
=21x-0.8
=
=（米）
故答案为：．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
