题目内容
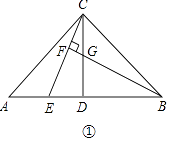
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
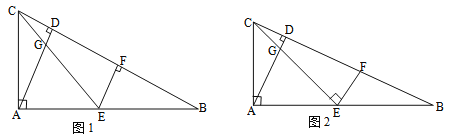
(1)如图1,若AC:AB=1:2,EF⊥CB,求证:EF=CD;
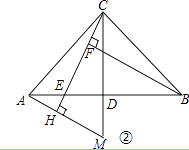
(2)如图2,若AC:AB=1: ![]() ,EF⊥CE,求EF: EG的值.
,EF⊥CE,求EF: EG的值.
【答案】(1)证明见解析;(2)![]()
【解析】(1)根据同角的余角相等得出∠CAD=∠B,根据AC:AB=1:2及点E为AB的中点,得出AC=BE,再利用AAS证明△ACD≌△BEF,即可得出EF=CD;
(2)作EH⊥AD于H,EQ⊥BC于Q,先证明四边形EQDH是矩形,得出∠QEH=90°,则∠FEQ=∠GEH,再由两角对应相等的两三角形相似证明△EFQ∽△EGH,得出EF:EG=EQ:EH,然后在△BEQ中,根据正弦函数的定义得出EQ=![]() BE,在△AEH中,根据余弦函数的定义得出EH=
BE,在△AEH中,根据余弦函数的定义得出EH=![]() AE,又BE=AE,进而求出EF:EG的值.
AE,又BE=AE,进而求出EF:EG的值.
解:(1)证明:如图所示,∵AC:AB=1:2,点E为AB的中点,∴AC=BE,
∵AD⊥BC,∠CAB=90°,
∴∠B+∠BAD=∠DAC+∠BAD=90°,∴∠B=∠DAC ,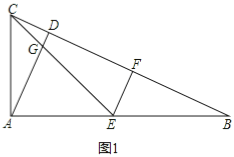
又∵AD⊥BC,EF⊥CB,∴∠ADC=∠BFE=90°,
∴△EFB≌△CDA(AAS)
∴EF=CD.
(2)过点E作EMBD,EN⊥AD,如图2所示,

∵AD⊥BC ∴∠NEM=90° ∵CE⊥EF ∴∠NEG=∠MEF
∵∠ENG=∠EMF=90°,∴△EMF∽△ENG,∴![]() ,
,
∵AD⊥BC,AC:AB=1: ![]() ,∴∠B=30°,∴∠NAE=60°
,∴∠B=30°,∴∠NAE=60°
∴EN=![]() AE,同理可得EM=
AE,同理可得EM=![]() BE,
BE,
∵点E为AB的中点,∴AE=BE,
∴![]() =
=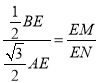 =
=![]() .
.
“点睛”本题考查了相似三角形的判定和性质、全等三角形的判定和性质、矩形的判定和性质,解直角三角形,综合性较强,有一定难度.解题的关键是作辅助线,构造相似三角形,并且证明四边形EQDH是矩形.