题目内容
【题目】为了丰富学生的课外活动,某校决定购买100个篮球和a(a>10)副羽毛球拍.经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副羽毛球拍贵25元,两个篮球与三副羽毛球拍的费用正好相等.经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球数超过80个,则购买羽毛球拍可打八折.
(1)设每个篮球x元,则每副羽毛球拍______元(用含x的代数表示);并求出每个篮球和每副羽毛球拍的价格分别是多少?
(2)请用含a的代数式分别表示出到甲商店和乙商店购买所花的费用;
(3)请你决策:在哪一家商店购买划算?(直接写出结论)
【答案】(1)(x-25),每个篮球的价格是75元,每副羽毛球拍的价格是50元;(2)到甲商店购买所花的费用为50a+7000(元); 到乙商店购买所花的费用为40a+7500(元); (3)当10<a<50时,在甲商店购买划算; 当a=50时,在甲、乙两个商店购买所花的费用一样; 当a>50时,在乙商店购买划算.
【解析】
(1)设每个篮球x元,则每副羽毛球拍(x-25)元,再根据题意列出方程求解即可;
(2)根据题意直接写出到甲商店和乙商店购买所花的费用即可;
(3)根据(2)中的表达式,求出到甲商店和乙商店购买所花的费用相等时的a值,再分类讨论即可.
(1)每幅羽毛球拍的价格是(x-25)元,
由题意得2x=3(x-25),解得x=75,则x-25=50,
则每个篮球的价格是75元,每副羽毛球拍的价格是50元;
(2)到甲商店购买所花的费用为:75×100+50![]() =50a+7000(元);
=50a+7000(元);
到乙商店购买所花的费用为:75×100+0.8×50×a=40a+7500(元);
(3)50a+7000=40a+7500,解得:a=50,
当10<a<50时,在甲商店购买划算;
当a=50时,在甲、乙两个商店购买所花的费用一样;
当a>50时,在乙商店购买划算.

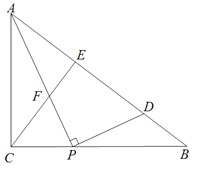
【题目】如图,Rt△ABC,∠C=90°,CA=CB=4![]() cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数
cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
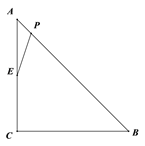
下面是小安的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①写出该函数的一条性质: ;
②当![]() 时,
时,![]() 的长度约为 cm.
的长度约为 cm.