题目内容
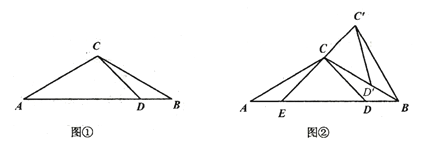
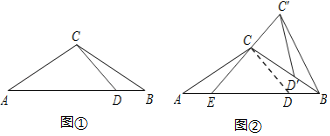
【题目】如图①,△ABC中,AC=BC,∠A=30°,点D在AB边上且∠ADC=45°.
(1)求∠BCD的度数;
(2)将图①中的△BCD绕点B顺时针旋转,得到△BC′D′.当点D′恰好落在BC边上时,如图②所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
【答案】(1)15°;(2)①75°;②答案见解析.
【解析】试题分析:(1)根据三角形外角性质,即可得到∠BCD=∠ADC﹣∠CBA=15°;
(2)①由旋转可得CB=C'B=AC,∠C'BD'=∠CBD=∠A=30°,再根据等腰三角形的性质,即可得到∠CC'B=∠C'CB=75°;
②先根据AC=C'B,∠C'BD'=∠A,得出∠CEB=∠C'CB﹣∠CBA=45°,进而得到∠ACE=∠CEB﹣∠A=15°,据此可得∠BC'D'=∠BCD=∠ACE,运用ASA即可判定△C'BD'≌△CAE.
试题解析:解:(1)∵AC=BC,∠A=30°,∴∠CBA=∠CAB=30°.∵∠ADC=45°,∴∠BCD=∠ADC﹣∠CBA=15°=∠BC'D';
(2)①由旋转可得CB=C'B=AC,∠C'BD'=∠CBD=∠A=30°,∴∠CC'B=∠C'CB=75°;
②证明:∵AC=C'B,∠C'BD'=∠A,∴∠CEB=∠C'CB﹣∠CBA=45°,∴∠ACE=∠CEB﹣∠A=15°,∴∠BC'D'=∠BCD=∠ACE.在△C'BD'和△CAE中,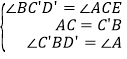 ,∴△C'BD'≌△CAE(ASA).
,∴△C'BD'≌△CAE(ASA).

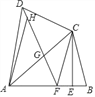
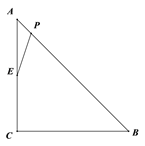
【题目】如图,Rt△ABC,∠C=90°,CA=CB=4![]() cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数
cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小安的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①写出该函数的一条性质: ;
②当![]() 时,
时,![]() 的长度约为 cm.
的长度约为 cm.