题目内容
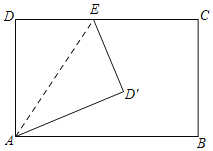
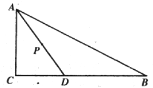
【题目】已知矩形ABCD,其中AD>AB,依题意先画出图形,然后解答问题.
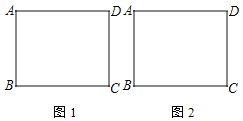
(1)F为DC边上一点,把△ADF沿AF折叠,使点D恰好落在BC上的点E处.在图1中先画出点E,再画出点F,若AB=8,AD=10,直接写出EF的长为 ;
(2)把△ADC沿对角线AC折叠,点D落在点E处,在图2先画出点E,AE交CB于点F,连接BE.求证:△BEF是等腰三角形.
【答案】(1)5;(2)见解析
【解析】
(1)在BC上截取AE=AD得点E,作AF垂直DE交CD于点F(或作∠AED的平分线AF交CD于点F,或作EF垂直AE交CD于点F等等);
(2)作DH垂直AC于点H,延长DH至点E,使HE=DH.方法一证明△ABE≌△CEB(SSS).方法二证明FA=FC即可解决问题.
(1)如图1,以A为圆心,AD长为半径作弧交BC于点E,作AF垂直DE交CD于点F,
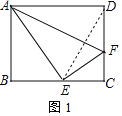
∵四边形ABCD是矩形,
∴AB=CD=8,AD=BC=10,∠B=∠C=90°,
在Rt△ABE中,BE![]() ,
,
∴EC=10﹣6=4,
根据折叠的性质知:EF=DF,
设EF=DF=x,则![]() ,
,
在Rt△EFC中,则有x2=(8﹣x)2+42,
解得 :x=5,
∴EF=5.
故答案为:5;
(2)证明:如图2,作DH垂直AC于点H,延长DH至点E,使HE=DH.
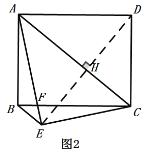
方法1:根据折叠的性质知:△ADC≌△AEC,
∴AD=AE=BC,AB=DC=EC,
在△ABE与△CEB中,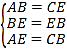 ,
,
∴△ABE≌△CEB(SSS),
∴∠AEB=∠CBE,
∴BF=EF,
∴△BEF是等腰三角形.
方法2:根据折叠的性质知:△ADC≌△AEC,
∴AD=AE=BC,∠DAC=∠EAC,
又∴AD∥BC,
∴∠DAC=∠ACB,
∴∠EAC=∠ACB,
∴FA=FC,
∴FE=FB,
∴△BEF是等腰三角形.

 阅读快车系列答案
阅读快车系列答案【题目】一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
A 类 | 50 | 25 |
B 类 | 200 | 20 |
C 类 | 400 | 15 |
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为( )
A.购买A类会员卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
【题目】为了解全区3000名九年级学生英语听力口语自动化考试成绩的情况,随机抽取了部分学生的成绩(满分30分且得分均为整数),制成下表:
分数段(x分分) | 0≤x≤18 | 19≤x≤21 | 22≤x≤24 | 25≤x≤27 | 28≤x≤30 |
人数 | 10 | 15 | 35 | 112 | 128 |
(1)填空:
①本次抽样调查共抽取了 名学生;
②学生成绩的中位数所在的分数段是 ;
③若用扇形统计图表示统计结果,则分数段为0≤x≤18的人数所对应扇形的圆心角为 °;
(2)如果将25分以上(含25分)定为优秀,请估计全区九年级考生成绩为优秀的人数.