Question

【题目】如图，在矩形ABCD中，AD＝8，AB＝14，E为DC上的一个点，将△ADE沿AE折叠，使得点D落在D'处，若以C、B、D'为顶点的三角形是等腰三角形，则DE的长为_____．

Answer 1

【答案】或

【解析】

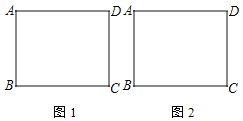
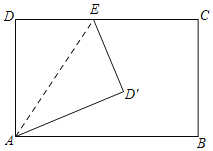
分三种情况讨论：①当CD'＝BD'时，如图1，连接DD'，由矩形的性质和等腰三角形的性质可得AB＝CD，∠DCD′＝∠ABD′，进而可利用SAS证明△DD′C≌△AD′B，可得DD′＝AD′，从而可得△ADD′是等边三角形，进一步即可得出∠DAE＝30°，然后解直角△ADE即可求出DE；

②当CD'＝CB时，如图2，连接AC，则AC易求，然后根据三角形的三边关系即可得出结论；

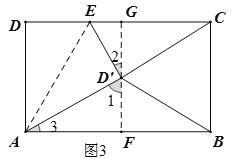
③当BD'＝BC时，如图3，过D'作AB的垂线，垂足为F，延长FD'交CD于G，则有AD'＝BD'=8，由等腰三角形的性质可得AF＝BF，根据勾股定理可得D'F，易证△AD'F∽△D'EG，然后根据相似三角形的性质即可求出D'E，进而可得答案．

解：①当CD'＝BD'时，则∠D′BC＝∠D′CB，如图1，连接DD'，由折叠性质得：AD＝AD′，∠DAE＝∠D′AE，

∵四边形ABCD是矩形，∴AB＝CD，∠ABC＝∠DCB＝90°，

∴∠DCD′＝∠ABD′，

∴△DD′C≌△AD′B（SAS），∴DD′＝AD′，

∴DD′＝AD′＝AD，

∴△ADD′是等边三角形，

∴∠DAD′＝60°，∴∠DAE＝30°，

则在直角△ADE中，；

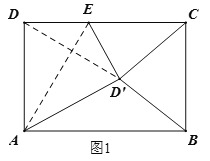
②当CD'＝CB时，如图2，连接AC，

由于AD'＝8，CD'＝8，而AC=＞8+8；

故这种情况不存在；

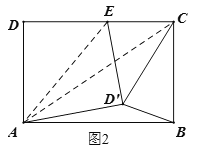
③当BD'＝BC时，如图3，过D'作AB的垂线，垂足为F，延长FD'交CD于G，

∵AD'＝AD=BC=BD'=8，∴AF＝BF=7，

则在直角△AFD'中，由勾股定理，得：D'F＝，

∵∠AFG=∠AD'E=∠EGF=90°，∴∠1+∠3=90°，∠1+∠2=90°，∴∠3=∠2，

∴△AD'F∽△D'EG，∴，

∴，解得：，即．

故答案为：或．