题目内容
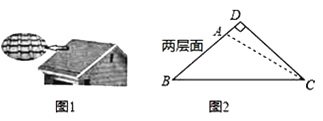
【题目】如图，在电线杆上的点
处引同样长度的拉线
，
固定电线杆
，在离电线杆6米处安置测角仪
（其中点
、
、
、
在同一条直线上），在
处测得电线杆上点处的仰角为
，测角仪的高为
米．
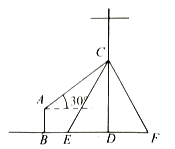
（1）求电线杆上点离地面的距离；
（2）若拉线，的长度之和为18米，求固定点和之间的距离．
【答案】（1）
米（2）
米
【解析】
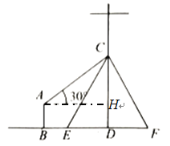
（1）过点A作AH⊥CD于点H，可得四边形ABDH为矩形，根据A处测得电线杆上C处得仰角为30°，在△ACH中求出CH的长度，从而得出CD的长；
（2）然后在Rt△CDE中求出DE的长度，根据等腰三角形的性质，可得出DF=DE，从而得出EF的长．
解：（1）过
作
于
，由条件知，
为矩形，
∴
，
．
在
中，
，即
，
∴
．∴
．
∴
为米．
（2）∵
，
，∴
，
在
中，
，，
∴
，
∵，
，∴
，
∴
，
∴
、
之间的距离为米．
练习册系列答案
相关题目
