题目内容
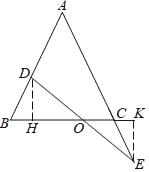
【题目】如图,△ABC中,AB=AC,D、E分别是AB及AC延长线上的点,且BD=CE,连接DE交BC于点O.过点D作DH⊥BC,过E作EK⊥BC,垂足分别为H、K.
(1)求证:DH=EK;
(2)求证:DO=EO.
【答案】(1)见解析;(2)见解析.
【解析】
(1)只要证明△BDH≌△CEK,即可解决问题;
(2)只要证明△DHO≌△EKO即可解决问题;
(1)∵DH⊥BC,EK⊥BC,
∴∠DHB=∠K=90°,
∵AB=AC,
∴∠B=∠ACB,
又∵∠ACB=∠ECK,
∴∠B=∠ECK,
在△BDH和△CEK中
∵∠ACB=∠ECK,∠B=∠ECK,BD=CE
∴△BDH≌△CEK(AAS).
∴DH=EK.
(2)∵DH⊥AC,EK⊥BC,
∴∠DHO=∠K=90°,
由(1)得EK=DH,
在△DHO和△EKO中,
∵∠DHO=∠K,∠DOH=∠EOK,DH=EK
∴△DHO≌△EKO(AAS),
∴DO=EO.

练习册系列答案
相关题目