Question

【题目】已知P为⊙O外一点，PA，PB为⊙O的切线，A、B为切点，∠P=70°，C为⊙O上一个动点，且不与A、B重合，则∠BCA=（　　）
A.35°、145°
B.110°、70°
C.55°、125°
D.110°

Answer 1

【答案】C
【解析】解：如图；连接OA、OB，则∠OAP=∠OBP=90°，
∴∠BOA=180°﹣∠P=110°，
∴∠AEB=∠AOB=55°；
∵四边形AEBF是⊙O的内接四边形，
∴∠AFB=180°﹣∠AEB=125°，
①当C点在优弧AB上运动时，∠BCA=∠AEB=55°；
②当C点在劣弧AB上运动时，∠BCA=∠AFB=125°；
故选C．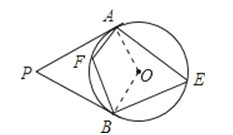

连接OA、OB，首先根据四边形内角和求出∠AOB的度数；由于C点的位置有两种情况，需分类讨论．