题目内容
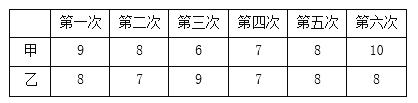
【题目】甲、乙两名同学分别进行6次射击训练，训练成绩（单位：环）如下表 对他们的训练成绩作如下分析，其中说法正确的是（ ）
A. 他们训练成绩的平均数相同
B. 他们训练成绩的中位数不同
C. 他们训练成绩的方差不同
D. 他们训练成绩的众数不同
【答案】C
【解析】
利用方差的定义、以及众数和中位数的定义分别计算得出答案．
解：∵甲6次射击的成绩从小到大排列为6、7、8、8、9、10，
∴甲成绩的平均数为
＝8（环），中位数为
＝8（环）、众数为8环，
方差为
×[（68）2＋（78）2＋2×（88）2＋（98）2＋（108）2]＝
（环2），
∵乙6次射击的成绩从小到大排列为：7、7、8、8、8、9，
∴乙成绩的平均数为
＝
，中位数为＝8（环）、众数为8环，
方差为×[2×（7）2＋3×（8）2＋（9）2]＝
（环2），
则甲、乙两人的平均成绩不相同、中位数和众数均相同，而方差不相同，
故选：C．
新课标同步训练系列答案
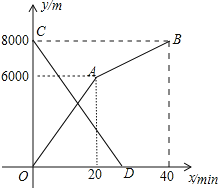
一线名师口算应用题天天练一本全系列答案【题目】某商店销售面向中考生的计数跳绳，每根成本为20元，销售的前40天内的日销售量m（根）与时间t（天）的关系如表．
时间t（天） | 1 | 3 | 8 | 10 | 26 | … |
日销售量m（件） | 51 | 49 | 44 | 42 | 26 | … |
前40天每天的价格y（元/件）与时间t（天）的函数关系式为：y=
t+25（1≤t≤40且t为整数）；
（1）认真分析表中的数据，用所学过的知识确定m（件）与t（天）之间是满足一次函数的关系还是二次函数的关系？并利用这些数据求m（件）与t（天）之间得函数关系式；
（2）请计算40天中哪一天的日销售利润最大，最大日销售利润是多少？
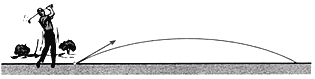
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度h（m）与它的飞行时间（s）满足二次函数关系，t与h的几组对应值如下表所示：
t（s） | 0 | 0.5 | 1 | 1.5 | 2 | … |
h（m） | 0 | 8.75 | 15 | 18.75 | 20 | … |
（1）求h与t之间的函数关系式（不要求写t的取值范围）；
（2）求小球飞行3s时的高度．
