题目内容
【题目】如图,在梯形ABCD中, ![]() ,
,![]() ,求DC的长.
,求DC的长.
【答案】解:如图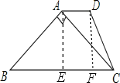
过A作AE⊥BC于E,过D作DF⊥BC于F,
则∠AEF=∠DFE=∠DFC=∠AEB=90°,AE∥DF,
∵AD∥BC,
∴四边形AEFD是矩形,
∴AE=DF,AD=EF=![]() ,
,
在Rt△BAC中,∠B=45°,BC=![]() ,
,
∴∠ACB=45°=∠B,
∴AB=AC,
由勾股定理得:AB=AC=4,
△BAC的面积S=![]() AB×AC=
AB×AC=![]() BC×AE,
BC×AE,
∴AE=![]()
DF=AE=![]() ,
,
∵AB=AC,AE⊥BC,
∴BE=CE=![]() BC=
BC=![]() ,
,
∴CF=![]() -
-![]() =
=![]() ,
,
在Rt△DFC中,DF=![]() ,CF=
,CF=![]() , 由勾股定理得:CD=
, 由勾股定理得:CD=![]()
【解析】过A作AE⊥BC于E,过D作DF⊥BC于F,得出矩形AEFD,求出AE=DF,AD=EF,求出AE、EC的长,求出CF长,即可求出答案.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.

练习册系列答案
相关题目