题目内容
【题目】在梯形ABCD中,AD∥BC,对角线AC和BD交于点O,下列条件中,能判断梯形ABCD是等腰梯形的是( )
A.∠BDC =∠BCD
B.∠ABC =∠DAB
C.∠ADB =∠DAC
D.∠AOB =∠BOC
【答案】C
【解析】根据等腰梯形的判定,逐一作出判断: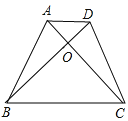
A.由∠BDC =∠BCD只能判断△BCD是等腰三角形,而不能判断梯形ABCD是等腰梯形;
B.由∠ABC =∠DAB和AD∥BC,可得∠ABC =∠DAB=900 , 是直角梯形,而不能判断梯形ABCD是等腰梯形;
C.由∠ADB =∠DAC,可得AO=OD,由AD∥BC,可得∠ADB =∠DBC,∠DAC =∠ACB,从而得到∠DBC =∠ACB,所以OB=OC,因此AC=DB,根据对角线相等的梯形是等腰梯形可判定梯形ABCD是等腰梯形;
D.由∠AOB =∠BOC只能判断梯形ABCD的对角线互相垂直,而不能判断梯形ABCD是等腰梯形。
故选C.
【考点精析】关于本题考查的等腰三角形的判定和等腰梯形的性质,需要了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等才能得出正确答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某生物课外活动小组的同学进行植物标本制作比赛,结果统计如下表:
每人所制 作标本数 | 2 | 4 | 6 | 8 | 10 |
人数 | 1 | 2 | 4 | 3 | 2 |
请根据表中信息,回答下列问题:
(1)该活动小组共有学生多少人?
(2)制作标本数在6个及以上的人数占小组总人数的百分比是多少?
(3)根据统计表制作一个合适的统计图来描述这次比赛的结果.





