题目内容
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,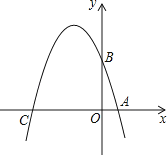
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c,
∵A(1,0)、B(0,3)、C(﹣4,0),
∴  ,
,
解得:a=﹣ ![]() ,b=﹣
,b=﹣ ![]() ,c=3,
,c=3,
∴经过A、B、C三点的抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+3
x+3
(2)
解:在平面直角坐标系xOy中存在一点P,使得以点A、B、C、P为顶点的四边形为菱形,理由为: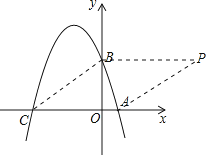
∵OB=3,OC=4,OA=1,
∴BC=AC=5,
当BP平行且等于AC时,四边形ACBP为菱形,
∴BP=AC=5,且点P到x轴的距离等于OB,
∴点P的坐标为(5,3),
当点P在第二、三象限时,以点A、B、C、P为顶点的四边形只能是平行四边形,不是菱形,则当点P的坐标为(5,3)时,以点A、B、C、P为顶点的四边形为菱形.
(3)
解:设直线PA的解析式为y=kx+b(k≠0),
∵A(1,0),P(5,3),
∴ ![]() ,
,
解得:k= ![]() ,b=﹣
,b=﹣ ![]() ,
,
∴直线PA的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
当点M与点P、A不在同一直线上时,根据三角形的三边关系|PM﹣AM|<PA,
当点M与点P、A在同一直线上时,|PM﹣AM|=PA,
∴当点M与点P、A在同一直线上时,|PM﹣AM|的值最大,即点M为直线PA与抛物线的交点,
解方程组 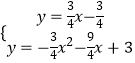 ,得
,得 ![]() 或
或 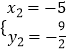 ,
,
∴点M的坐标为(1,0)或(﹣5,﹣ ![]() )时,|PM﹣AM|的值最大,此时|PM﹣AM|的最大值为5.
)时,|PM﹣AM|的值最大,此时|PM﹣AM|的最大值为5.
【解析】(1)设抛物线的解析式为y=ax2+bx+c,把A,B,C三点坐标代入求出a,b,c的值,即可确定出所求抛物线解析式;
(2)在平面直角坐标系xOy中存在一点P,使得以点A、B、C、P为顶点的四边形为菱形,理由为:根据OA,OB,OC的长,利用勾股定理求出BC与AC的长相等,只有当BP与AC平行且相等时,四边形ACBP为菱形,可得出BP的长,由OB的长确定出P的纵坐标,确定出P坐标,当点P在第二、三象限时,以点A、B、C、P为顶点的四边形只能是平行四边形,不是菱形;
(3)利用待定系数法确定出直线PA解析式,当点M与点P、A不在同一直线上时,根据三角形的三边关系|PM﹣AM|<PA,当点M与点P、A在同一直线上时,|PM﹣AM|=PA,
当点M与点P、A在同一直线上时,|PM﹣AM|的值最大,即点M为直线PA与抛物线的交点,联立直线AP与抛物线解析式,求出当|PM﹣AM|的最大值时M坐标,确定出|PM﹣AM|的最大值即可.此题属于二次函数综合题,涉及的知识有:二次函数的性质,待定系数法确定抛物线解析式、一次函数解析式,菱形的判定,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键.

【题目】湖州某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 15 | 12 |
月污水处理能力(吨/月) | 250 | 200 |
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.