Question

在矩形ABCD中，点O在对角线BD上，以OD为半径的⊙O与AD、BD分别交于点E、F，且∠ABE=∠DBC．
（1）求证：BE与⊙O相切；
（2）若sin∠ABE=

1

3

，CD=2，求⊙O的半径．

Answer 1

（1）证明：连接OE．
∵四边形ABCD是矩形，
∴AD∥BC，∠C=∠A=90°．
∴∠3=∠DBC，∠ABE+∠1=90°．
∵OD=OE，∠ABE=∠DBC，
∴∠2=∠3=∠ABE．
∴∠2+∠1=90°．
∴∠BEO=90°．
∵点E在⊙O上，
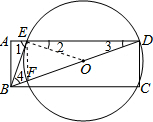∴BE与⊙O相切；

（2）∵∠ABE=∠DBC，
∴sin∠DBC=sin∠ABE=

1

3

．
∵DC=2，∠C=90°，
∴DB=6，
∵∠A=90°，
∴BE=3AE．
∵AB=CD=2，
利用勾股定理，得AE=

2

2

，AD=4

2

．
∴DE=

7 2

2

．
连接EF．
∵DF是⊙O的直径，
∴∠DEF=∠A=90°．
∴AB∥EF．
∴△DEF∽△DAB．
∴

DE

AD

=

DF

BD

．
∴

7 2 2

4 2

=

DF

6

．
∴DF=

21

4

．
∴⊙O的半径为

21

8

．