题目内容
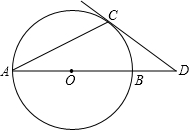
如图，已知AC切⊙O于A，AB为直径，C为⊙O外一点，BC交⊙O于点D，AC=6，BD=5，连接AD．
（1）证明：△CAD∽△CBA；（2）求线段DC的长．
（1）证明：△CAD∽△CBA；（2）求线段DC的长．
证明：（1）∵AB是直径，
∴∠ADB=90°．
又∵CA是切线，
∴BA⊥AC，∴∠BAC=90°．
∴∠BAC=∠CDA=90°．
又∵∠BCA=∠DCA，
∴△CAD∽△CBA．
（2）由（1）知△CAD∽△CBA，
∴
=
．
设DC=x，
则
=
，
即x2+5x-36=0，
解得x=4或x=-9（舍去），
∴CD的长为4．
∴∠ADB=90°．
又∵CA是切线，
∴BA⊥AC，∴∠BAC=90°．
∴∠BAC=∠CDA=90°．
又∵∠BCA=∠DCA，
∴△CAD∽△CBA．
（2）由（1）知△CAD∽△CBA，
∴
| DC |
| CA |
| AC |
| CB |
设DC=x，
则
| x |
| 6 |
| 6 |
| x+5 |
即x2+5x-36=0，
解得x=4或x=-9（舍去），
∴CD的长为4．
练习册系列答案
阅读快车系列答案
相关题目
AC交BC于点D，在OD的延长线上取一点E，连接EB，使∠OEB=∠ABC．
接AB，过O1作O1C⊥BA于C，连接CO2．已知PA=
