Question

【题目】在中，，点为边的中点

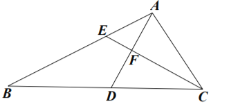
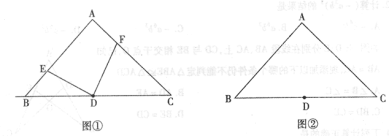
（1）如图①，点分别为边上的点，且．若，则 ；若，则四边形的面积为

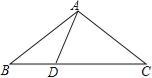
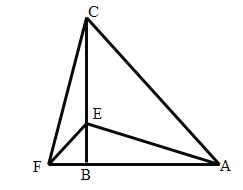
（2）若点分别为延长线上的点，且，那么吗?请利用图②说明理由．

Answer 1

【答案】（1）7, 25cm2；（2），见解析

【解析】

（1）连接AD，易知△ABC是等腰直角三角形，根据等腰直角三角形的性质可得AD＝BD，∠FAD＝∠B＝45°,根据等角替换可得∠ADF＝∠BDE，可得△BDE≌△ADF，根据全等三角形的性质可得BE＝AF，进而可求CF，把四边形AEDF分割成△ADE和△ADF，即可求解．

（2）连接AD，根据等腰直角三角形的性质可得BD＝AD，∠ABC＝∠DAC＝45°，再根据平角性质可得∠EBD＝∠FAD＝135°，根据等角替换可得∠ADF＝∠BDE，根据全等三角形的判定证得△BDE≌△ADF，进而求证BE＝AF．

（1）如图①，连接AD

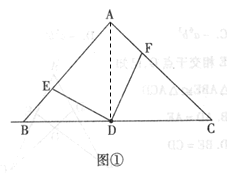
∵∠BAC＝90°，AB＝AC，

∴△ABC是等腰直角三角形，

∴∠B＝45°，

∵D是BC的中点，

∴AD⊥BD，∠BAD＝∠FAD＝45°，

∴∠FAD＝∠B＝45°，

∵∠BDE＋∠EDA＝∠EDA＋∠ADF＝90°，

∴∠BDE＝∠ADF，

∵∠BAD＝∠B＝45°，

∴AD＝BD，

在△BDE和△ADF中

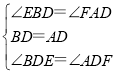
∴△BDE≌△ADF（ASA）

∴BE＝AF

∵AB＝AC＝10cm，BE＝3cm，

∴AF＝BE＝3cm

∴CF＝10－3＝7cm,

∵S△ABD＝S△ACD＝S△ABC，

即S△BDE＋S△ADE＝S△ADF＋S△CDF

又∵△BDE≌△ADF

∴S△BDE＝S△ADF

∴S△ADE＝S△CDF，

∴S△ADE＋S△ADF＝S△ABC＝×10×10＝25cm2,

即四边形AEDF的面积为25cm2

（2）结论：BE＝AF

理由：如图②连接AD，

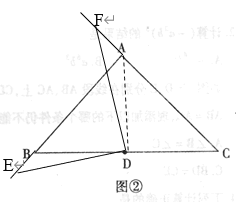
易知∠BDA＝∠EDF＝90°，

∴∠BDE＋∠BDF＝∠BDF＋∠ADF，

∴∠BDE＝∠ADF，

又∵D是BC的中点，△ABC是等腰直角三角形，

∴BD＝AD，∠ABC＝∠DAC＝45°，

∴∠EBD＝∠FAD＝180°－45°＝135°，

∴△BDE≌△ADF（ASA），

∴BE＝AF