题目内容
【题目】(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
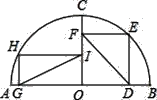
(2)如图:![]() =
=![]() ,D、E分别是半径OA和OB的中点.求证:CD=CE.
,D、E分别是半径OA和OB的中点.求证:CD=CE.
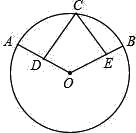
【答案】(1)最大值为17cm,最小值为7cm;(2)证明见解析.
【解析】
(1)先由直径为10cm,可求半径为5cm,PA取得最大值是当点P在线段OA的延长线上时,由OA=12cm,可得PA的最大值为12+5=17cm,PA取得最小值是当点P在线段OA上时,可得PA的最小值为12-5=7cm;
(2)连接CO,由D、E分别是半径OA和OB的中点,可得OD=OE,由![]() =
=![]() ,可得∠COD=∠COE,然后根据SAS可证△COD≌△COE,然后根据全等三角形的对应边相等即可得到CD=CE.
,可得∠COD=∠COE,然后根据SAS可证△COD≌△COE,然后根据全等三角形的对应边相等即可得到CD=CE.
(1)解:∵⊙O的直径为10cm,
∴⊙O的半径为10÷2=5(cm),
当点P在线段OA的延长线上时,PA取得最大值,当点P在线段OA上时,PA取得最小值
∵OA=12cm,
∴PA的最大值为12+5=17cm,PA的最小值为12﹣5=7cm;
(2)证明:连接CO,如图所示,
∵OA=OB,且D、E分别是半径OA和OB的中点,
∴OD=OE,
又∵![]() =
=![]() ,
,
∴∠COD=∠COE,
在△COD和△COE中,
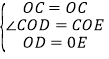 ,
,
∴△COD≌△COE(SAS),
∴CD=CE.

练习册系列答案
相关题目