题目内容
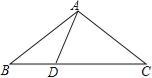
【题目】如图,在△ABC中,AB=AC=10,sinC=![]() ,点D是BC上一点,且DC=AC.
,点D是BC上一点,且DC=AC.
(1)求BD的长;
(2)求tan∠BAD.
【答案】(1)6.(2)![]() .
.
【解析】
试题(1)过点A作AE⊥BC于点E,求出CE,BE,再由CD=AC,可求出BD的长度.
(2)过点D作DF⊥AB于点F,在Rt△BDF中求出DF,BF,继而可得AF,从而可求tan∠BAD.
试题解析:(1)过点A作AE⊥BC于点E,
∵AB=AC,
∴BE=CE,
在Rt△ACE中,AC=10,sin∠C=![]() ,
,
∴AE=6,
∴CE=![]() =8,
=8,
∴CD=2CE=16,
∴BD=BC-BD=BC-AC=6.
(2)过点D作DF⊥AB于点F,

在Rt△BDF中,BD=6,sin∠B=sin∠C=![]() ,
,
∴DF=![]() ,
,
∴BF=![]() ,
,
∴AF=AB-BF=![]() ,
,
∴tan∠BAD=![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目