Question

【题目】如图，在中，为三角形的角平分线，于点交于点

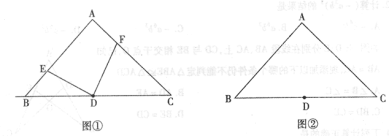
（1）若，直接写出 度

（2）若，

①求证：

②若，直接写出 （用含的式子表示）

Answer 1

【答案】（1）；（2）①见详解；②

【解析】

（1）由三角形内角和定理和角平分线定义即可得出答案；

（2）①证明，得出BE=CE，过点A作交CE与点H，则，得出AH=AC，，得出AE=HE，由等腰三角形的性质可得出HF=CF，即可得出结论；

②证明，得出AH=DC，求出HF=CF=a，HE=HF-EF=a-b，CE=a+b，由得出，进而得出结论．

解：（1）∵，

∴，

∵为三角形的角平分线，

∴，

∵，

∴，

∴．

故答案为：；

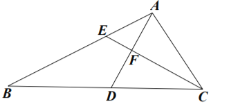
（2）①证明：∵

∴

∴

过点A作交CE与点H，如图所示：

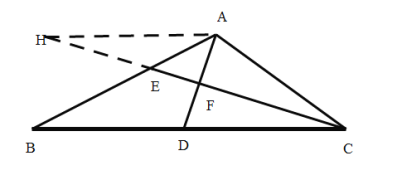
则

∴AH=AC，

∴AE=HE

∵

∴HF=CF

∴AB=HC=2CF；

②在和中，

∴

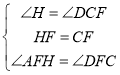
∴AH=DC

∵

∴，由①得，

∵

∴

∴

∴．

故答案为：．