Question

【题目】如图，在中，是高线，、是角平分线，它们相交于点，，，求与的度数．

Answer 1

【答案】∠EAD=5°，∠BOA=125°

【解析】

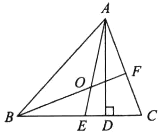
因为AD是高，所以∠ADC=90°，又因为∠C=70°，求出∠DAC度数，根据∠EAD=∠EAC-∠DAC可求∠EAD；因为∠BAC=50°，∠C=70°，所以∠BAO=25°，∠ABC=60°，BF是∠ABC的角平分线，则∠ABO=30°，故∠BOA的度数可求．

∵AD⊥BC
∴∠ADC=90°
∵∠C=70°
∴∠DAC=180°-90°-70°=20°，
∵AE平分∠BAC，
∴∠CAE=×50°=25°
∴∠EAD=∠EAC-∠DAC=25°-20°=5°；
∵∠BAC=50°，∠C=70°
∴∠BAO=25°，∠ABC=60°
∵BF是∠ABC的角平分线
∴∠ABO=30°
∴∠BOA=180°-∠BAO-∠ABO=180°-25°-30°=125°．