题目内容
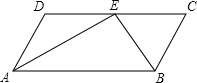
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
【答案】D
【解析】
根据SAS证△ABD≌△EBC,可得∠BCE=∠BDA,结合∠BCD=∠BDC可得①②正确;根据角的和差以及三角形外角的性质可得∠DCE=∠DAE,即AE=EC,由AD=EC,即可得③正确;过E作EG⊥BC于G点,证明Rt△BEG≌Rt△BEF和Rt△CEG≌Rt△AEF,得到BG=BF和AF=CG,利用线段和差即可得到④正确.
解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
∴在△ABD和△EBC中,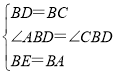 ,
,
∴△ABD≌△EBC(SAS),①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC.③正确;
④过E作EG⊥BC于G点,
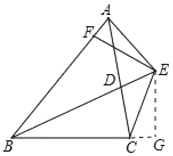
∵E是∠ABC的角平分线BD上的点,且EF⊥AB,
∴EF=EG(角平分线上的点到角的两边的距离相等),
∵在Rt△BEG和Rt△BEF中,![]() ,
,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
∵在Rt△CEG和Rt△AFE中,![]() ,
,
∴Rt△CEG≌Rt△AEF(HL),
∴AF=CG,
∴BA+BC=BF+FA+BGCG=BF+BG=2BF,④正确.
故选D.