题目内容
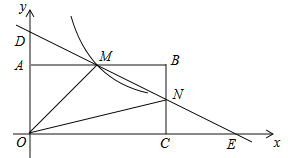
【题目】如图,在真角坐标系中,矩形0ABC的顶点A,C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N.
(1)求直线DE的函数表达式和点M,N的坐标;
(2)若函数y=![]() (k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(3)求△OMN的面积S;
(4)若函教y=![]() (k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.
(k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.

【答案】(1)y=-![]() x+3,M(2,2),N(4,1);
x+3,M(2,2),N(4,1);
(2)y=![]() ,点N在反比例函数图象上;
,点N在反比例函数图象上;
(3)3;
(4)k<0或0<k<4或k>8.
【解析】试题分析:(1)利用待定系数法即可求得直线DE的解析式,然后根据M的纵坐标是2,N的横坐标是4,即可求得M、N的坐标;
(2)利用待定系数即可求得反比例函数的解析式,然后把N的坐标代入解析式检验即可判断是否在反比例函数的图象上;
(3)根据△OMN的面积S=S梯形OCBM﹣S△OCN﹣S△BMN即可求解;
(4)根据经过M、N的反比例的函数的解析式,以及经过B的反比例函数的解析式,即可直接写出k的范围.
试题解析:解:(1)设直线DE的解析式是y=kx+b,根据题意得: ![]() ,解得:
,解得: 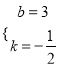 ,则直线DE的解析式是:y=﹣
,则直线DE的解析式是:y=﹣![]() x+3,令y=2,得到2=﹣
x+3,令y=2,得到2=﹣![]() x+3,解得:x=2,则M的坐标是(2,2),令x=4,解得:x=﹣2+3=1,则N的坐标是(4,1);
x+3,解得:x=2,则M的坐标是(2,2),令x=4,解得:x=﹣2+3=1,则N的坐标是(4,1);
(2)把(2,2)代入![]() 得;k=4,则反比例函数的解析式是:
得;k=4,则反比例函数的解析式是: ![]() ,当x=4时,y=1,则N在
,当x=4时,y=1,则N在![]() 的图象上;
的图象上;
(3)S梯形OCBM=![]() (BM+OC)BC=
(BM+OC)BC=![]() (2+4)2=6,S△OCN=
(2+4)2=6,S△OCN=![]() OCCN=
OCCN=![]() ×4×1=2,S△BMN=
×4×1=2,S△BMN=![]() BNBM=
BNBM=![]() ×1×2=1,则△OMN的面积S=6﹣2﹣1=3;
×1×2=1,则△OMN的面积S=6﹣2﹣1=3;
(4)经过M的反比例函数的解析式是: ![]() ,同时经过点N,则当0<k<4时,函数与△BNM没有交点;
,同时经过点N,则当0<k<4时,函数与△BNM没有交点;
经过点B的反比例函数的解析式是: ![]() ,则当k>8时,函数与△BMN没有交点;
,则当k>8时,函数与△BMN没有交点;
当k<0时,函数图象在二、四象限,则与△BMN没有交点.
故k的范围是:0<k<4或k>8或k<0.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案