Question

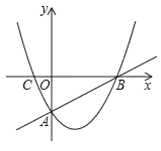
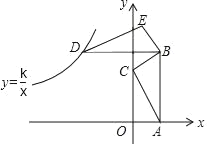
【题目】如图，在平面直角坐标系中，△ABC的顶点A和C分别在x轴、y轴的正半轴上，且AB∥y轴，AB＝4，△ABC的面积为2，将△ABC以点B为旋转中心，顺时针旋转90°得到△DBE，一反比例函数图象恰好过点D时，则此反比例函数解析式是_____．

Answer 1

【答案】y＝﹣．

【解析】

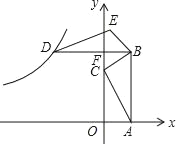
先根据三角形的面积公式求得OA的长，得到点B的坐标，再根据旋转的性质得BD＝BA＝4，∠DBA＝90°，则BD∥x轴，再求出D点的坐标，然后利用待定系数法求出反比例函数解析式．

解：∵AB∥y轴，AB＝4，△ABC的面积为2，

∴S△ABC＝ABOA＝×4×OA＝2OA＝2，

∴OA＝1，

∴B（1，4）．

∵将△ABC以点B为旋转中心，顺时针旋转90°得到△DBE，

∴AB＝BD＝4，∠ABD＝90°，

∴DB∥x轴，

设DB与y轴交于点F，

∴DF＝DB﹣BF＝4﹣1＝3，

∴D（﹣3，4），

设反比例解析式为y＝，

∴k＝﹣3×4＝﹣12．

∴此反比例函数解析式是y＝﹣．

故答案为y＝﹣．