��Ŀ����
����Ŀ���ڡ�ABC�У���ABΪб�ߣ���ֱ�ǡ�ABD��ʹ��D���ڡ�ABC�ڣ���ADB=90�㣮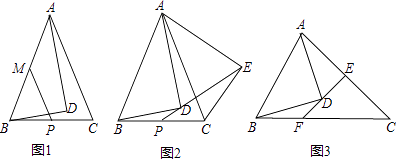
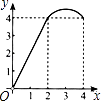
��1����ͼ1����AB=AC����DBA=60�㣬AD=7 ![]() ����P��M�ֱ�ΪBC��AB�ߵ��е㣬����PM�����߶�PM�ij���
����P��M�ֱ�ΪBC��AB�ߵ��е㣬����PM�����߶�PM�ij���
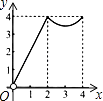
��2����ͼ2����AB=AC���ѡ�ABD�Ƶ�A��ʱ����תһ���Ƕȣ��õ���ACE������ED���ӳ���BC�ڵ�P����֤��BP=CP��
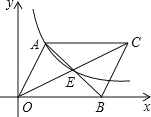
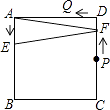
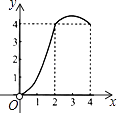
��3����ͼ3����AD=BD������D��ֱ�߽�AC�ڵ�E����BC�ڵ�F��EF��AC����AE=EC����ֱ��д���߶�BF��FC��AD֮��Ĺ�ϵ������Ҫ֤������
���𰸡�
��1��
�⣺��ͼ1�У�

�ߡ�ADB=90�㣬��DBA=60�㣬AD=7 ![]() ��
��
���BAD=30�㣬
��AB=2BD����BD=a����AB=2a��
��AB2=BD2+AD2��
�ࣨ2a��2=a2+��7 ![]() ��2��
��2��
��a=7��
��AB=AC=14��
��AM=MB��PB=PC��
��PM= ![]() AC=7
AC=7
��2��
֤������ͼ2�У���ED�Ͻ�ȡEQ=DP������CQ��

��AD=AE��
���1=��2��
�ߡ�ADB=��AEC=90�㣬
���1+��3=90�㣬��2+��4=90�㣬
���3=��4��
��BD=EC��
���EQC�ա�DPB��
��CQ=BP����QCE=��DBP��
�ߡ�CQP=��3+��QCE����CPQ=��4+��DBP��
���CQP=��CPQ��
��CQ=PC��
��PB=PC��
��3��
�⣺���ۣ�2AD2=FB2+CF2��
���ɣ���ͼ3�У�����AF��BD��N������CD�ӳ���H��

��EA=EC��EF��AC��
��DA=DC��
�ߡ�ADB=90�㣬DA=DB��
��DA=DC=DB�����DBA=��DAB=45�㣬AB= ![]() AD��
AD��
���DAC=��DCA����DBC=��DCB��
�ߡ�ADH=��DAC+��ACD����BDH����DBC+��DCB��
���ADB=2��ACD+2��DCB=90�㣬
���ACF=45�㣬
��FA=FC��
���FAC=��FCA=45�㣬
���AFC=90��
�ߡ�AND=��BNF����ADN=��BFN=90�㣬
���AND�ס�BNF��
�� ![]() ��
��
�� ![]() ���ߡ�ANB=��DNF��
���ߡ�ANB=��DNF��
���ANB�ס�DNF��
���DFN=��ABD=45�㣬
��FE��AC��AE=EC��
��FA=FC����AFE=��CFE=45�㣬
���AFC=��AFB=90�㣬
��AB2=BF2+AF2��
��2AD2=BF2+CF2
����������1������ֱ��������30�Ƚ��������AB���ٸ�����������λ�߶����������PM����2����ͼ2�У���ED�Ͻ�ȡEQ=DP������CQ������֤����EQC�ա�DPB���Ƴ�QC=PB����֤��QC=PC���ɽ�����⣮��3�����ۣ�2AD2=FB2+CF2 �� ��ͼ3�У�����AF��BD��N���ɡ�AND�ס�BNF���Ƴ� ![]() ���Ƴ�
���Ƴ� ![]() ���֡�ANB=��DNF���Ƴ���ANB�ס�DNF���ӡ�DFN=��ABD=45�㣬��RtABF�����ù��ɶ�������֤����
���֡�ANB=��DNF���Ƴ���ANB�ס�DNF���ӡ�DFN=��ABD=45�㣬��RtABF�����ù��ɶ�������֤����
�����㾫����������Ŀ����֪���������ù��ɶ����ĸ������������λ�߶��������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����������������е���߶ν��������ε���λ������������λ�߶����������ε���λ��ƽ���������εĵ����ߣ��ҵ��ڵ����ߵ�һ�룮