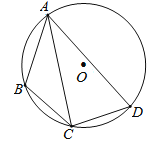
[题目]如图.在⊙O的内接四边形ABCD中.AB=3.AD=5.∠BAD=60°.点C为弧BD的中点.则AC的长是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在⊙O的内接四边形ABCD中，AB=3，AD=5，∠BAD=60°，点C为弧BD的中点，则AC的长是．

【答案】．

【解析】

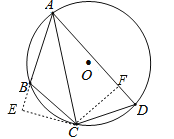
试题分析：过C作CE⊥AB于E，CF⊥AD于F，则∠E=∠CFD=∠CFA=90°，∵点C为弧BD的中点，∴，∴∠BAC=∠DAC，BC=CD，∵CE⊥AB，CF⊥AD，∴CE=CF，∵A、B、C、D四点共圆，∴∠D=∠CBE，在△CBE和△CDF中，∵∠CBE=∠D，∠E=∠CFD，CE=CF，∴△CBE≌△CDF，∴BE=DF，在△AEC和△AFC中，∵∠E=∠AFC，∠EAC=∠FAC，AC=AC，∴△AEC≌△AFC，∴AE=AF，设BE=DF=x，∵AB=3，AD=5，∴AE=AF=x+3，∴5=x+3+x，解得：x=1，即AE=4，∴AC==，故答案为：．

练习册系列答案

已知：如图，∠AOC=∠BOC，点P在OC上，求证：．

请你补全已知和求证，并写出证明过程．

【题目】质地均匀的骰子六个面分别刻有1到6的点数，掷两次骰子，得到向上一面的两个点数，则下列事件中，发生可能性最大的是（　　）
A.点数都是偶数
B.点数的和为奇数
C.点数的和小于13
D.点数的和小于2

【题目】某中学初一（二）班5位教师决定带领本班a名学生在五一期间在元旦期间去珠海长隆海洋王国旅游，每张票的价格为350元，A旅行社的收费标准为：教师全价，学生半价；而B旅行社的收费标准为：不分教师、学生，一律六折优惠．
（1）分别用代数式表示参加这两家旅行社所需的费用；
A旅行社所需费用为元，B旅行社所需费用为元，
（2）如果这5位教师要带领该班30名学生参加旅游，你认为选择哪一家旅行社较为合算，为什么？

【题目】设a＞b，则下列各式中不能成立的是（）
A.a+3＞b+3
B.a﹣4＞b﹣4
C.2a＞2b
D.﹣ ＞﹣

【题目】完成下列证明：
如图，已知DE⊥AC于点E，BC⊥AC于点C，FG⊥AB于点G，∠1=∠2，求证：CD⊥AB．

证明：∵DE⊥AC，BC⊥AC（已知），
∴DE∥（），
∴∠2=（两直线平行，内错角相等），
∵∠1=∠2，（已知），
∴∠1=（），
∴GF∥CD（），
∵FG⊥AB（已知），
∴CD⊥AB．