题目内容
【题目】
【发现】
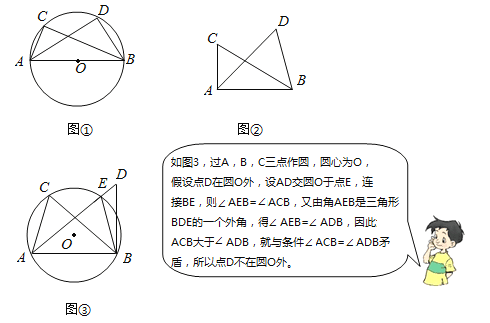
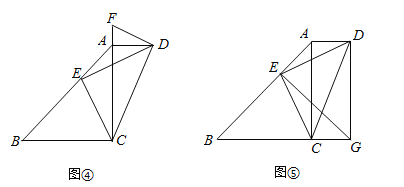
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
【思考】
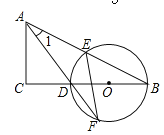
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?
请证明点D也不在⊙O内.
【应用】
利用【发现】和【思考】中的结论解决问题:若四边形ABCD中,AD∥BC,∠CAD=90°,点E在边AB上,CE⊥DE.
(1)作∠ADF=∠AED,交CA的延长线于点F(如图④),求证:DF为Rt△ACD的外接圆的切线;
(2)如图⑤,点G在BC的延长线上,∠BGE=∠BAC,已知sin∠AED=![]() ,AD=1,求DG的长.
,AD=1,求DG的长.
【答案】【思考】证明见试题解析;【应用】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:【思考】假设点D在⊙O内,由圆周角定理及三角形外角的性质,可证得与条件相矛盾的结论,从而证得点D不在⊙O内;
【应用】(1)作出RT△ACD的外接圆,由发现可得点E在⊙O上,则∠ACD=∠FDA,又∠ACD+∠ADC=90°,有∠FDA+∠ADC=90°,即可得出DF是圆的切线;
(2)由【发现】和【思考】可得点G在过C、A、E三点的圆O上,证明四边形AOGD是矩形,由已知条件解直角三角形ACD可得AC的长,即DG的长.
试题解析:【思考】如图1,假设点D在⊙O内,延长AD交⊙O于点E,连接BE,则∠AEB=∠ACB,∵∠ADE是△BDE的外角,∴∠ADB>∠AEB,∴∠ADB>∠ACB,因此,∠ADB>∠ACB这与条件∠ACB=∠ADB矛盾,所以点D也不在⊙O内,所以点D即不在⊙O内,也不在⊙O外,点D在⊙O上;
【应用】
(1)如图2,取CD的中点O,则点O是RT△ACD的外心,∵∠CAD=∠DEC=90°,∴点E在⊙O上,∴∠ACD=∠AED,∵∠FDA=∠AED,∴∠ACD=∠FDA,∵∠DAC=90°,∴∠ACD+∠ADC=90°,∴∠FDA+∠ADC=90°,∴OD⊥DF,∴DF为Rt△ACD的外接圆的切线;
(2)∵∠BGE=∠BAC,∴点G在过C、A、E三点的圆上,如图3,又∵过C、A、E三点的圆是RT△ACD的外接圆,即⊙O,∴点G在⊙O上,∵CD是直径,∴∠DGC=90°,∵AD∥BC,∴∠ADG=90°,∵∠DAC=90°,∴四边形ACGD是矩形,∴DG=AC,∵sin∠AED=![]() ,∠ACD=∠AED,∴sin∠ACD=
,∠ACD=∠AED,∴sin∠ACD=![]() ,在RT△ACD中,AD=1,∴
,在RT△ACD中,AD=1,∴![]() =
=![]() ,∴CD=
,∴CD=![]() ,∴AC=
,∴AC=![]() =
=![]() ,∴DG=
,∴DG=![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“車”字朝上的频数 | 14 | 18 | 38 | 47 | 52 |
| 78 | 88 |
相应的频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 |
|
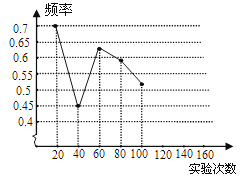
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
(3)在(2)的基础上,进一步估计:将该“車”字棋子,按照实验要求连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为多少?
【题目】股民老黄上星期五买进某股票1000股,每股35元,下表为本周内每日该股票的涨跌情况(单位:元)(注:用正数记股价比前一日上升数,用负数记股价比前一日下降数)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +2.4 | -0.8 | -2.9 | +0.5 | +2.1 |
(1)星期四收盘时,每股是多少元?
(2)本周内最高价每股多少元?最低价每股多少元?
(3)根据交易规则,老黄买进股票时需付0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果老黄在星期五收盘前将全部股票卖出,他的收益情况如何?