题目内容
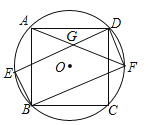
【题目】正方形ABCD内接于⊙O,如图所示,在劣弧![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
(1)四边形EBFD是矩形;
(2)DG=BE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°,∠BFD=∠BCD=90°,∠EDF=90°,进而得出答案;
(2)直接利用正方形的性质![]() 的度数是90°,进而得出BE=DF,则BE=DG.
的度数是90°,进而得出BE=DF,则BE=DG.
试题解析:(1)∵正方形ABCD内接于⊙O,∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,又∵DF∥BE,∴∠EDF+∠BED=180°,∴∠EDF=90°,∴四边形EBFD是矩形;
(2))∵正方形ABCD内接于⊙O,∴![]() 的度数是90°,∴∠AFD=45°,又∵∠GDF=90°,∴∠DGF=∠DFC=45°,∴DG=DF,又∵在矩形EBFD中,BE=DF,∴BE=DG.
的度数是90°,∴∠AFD=45°,又∵∠GDF=90°,∴∠DGF=∠DFC=45°,∴DG=DF,又∵在矩形EBFD中,BE=DF,∴BE=DG.

练习册系列答案
相关题目