Question

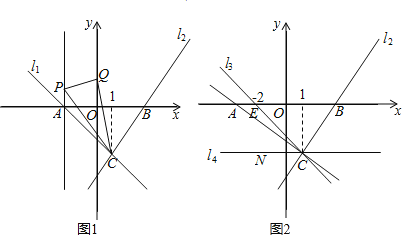
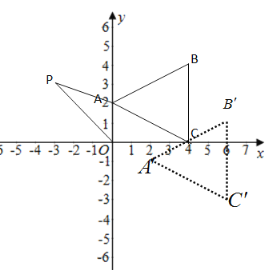
【题目】如图，△ABC在直角坐标系中，

（1）若把△ABC向右平移2个单位，再向下平移3个单位得到△A′B′C′，写出 A′、B′、C′的坐标，并在图中画出平移后图形．

（2）如果在第二象限内有一点P（m，3），四边形ACOP的面积为 （用含m的式子表示）

（3）在（2）的条件下，是否存在点P，使四边形ACOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）A′（2，-1）、B′（6，1）、C′（6，-3），见解析；（2）S四边形ABOP=4﹣m；（3）存在，点P（﹣4，3）使S四边形ABOP=S△ABC．

【解析】

（1）利用平移的性质，描出A、B、C平移后的点，再顺次连接即可；

（2）S四边形ACOP=S△ACO+S△APO，利用各点的坐标以及三角形的面积公式即可求得；

（3）求出S△ABC的面积，再利用S四边形ACOP=S△ABC即可求出m的值，即可得出点P的坐标.

解：（1）平移得到△如图所示

A′（2，-1）、B′（6，1）、C′（6，-3）

（2）四边形ACOP的面积为 （4-m）

∵S△ACO=×2×4=4，S△APO=×2×（﹣m）=﹣m，

∴S四边形ACOP=S△ACO+S△APO=4+（﹣m）=4﹣m，

即S四边形ACOP=4﹣m；

（3）因为S△ABC=×4×4=8，

∵S四边形ACOP=S△ABC

∴4﹣m=8，

则 m=﹣4，

所以存在点P（﹣4，3）使S四边形ACOP=S△ABC．