题目内容
【题目】已知直线l1:y=﹣x+b与x轴交于点A,直线l2:y=![]() x﹣
x﹣![]() 与x轴交于点B,直线l1、l2交与点C,且C点的横坐标为1.
与x轴交于点B,直线l1、l2交与点C,且C点的横坐标为1.
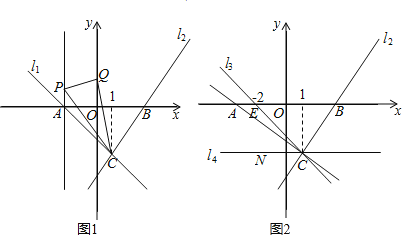
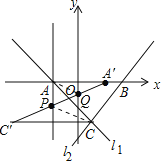
(1)如图,过点A作x轴的垂线,若点P(x,2)为垂线上的一个点,Q是y轴上一动点,若S△CPQ=5,求此时点Q的坐标;
(2)若P在过A作x轴的垂线上,点Q为y轴上的一个动点,当CP+PQ+QA的值最小时,求此时P的坐标;
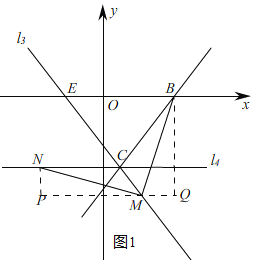
(3)如图,点E的坐标为(﹣2,0),将直线l1绕点C旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M点为直角顶点的等腰直角三角形,若存在, 求出N点的坐标;若不存在,请说明理由.
【答案】(1)Q的坐标为(0,0)或(0,-5);(2)点P的坐标为(﹣3,﹣![]() );(3)①点N的坐标为(﹣16,﹣4),②点N的坐标为(﹣
);(3)①点N的坐标为(﹣16,﹣4),②点N的坐标为(﹣![]() ,﹣4)或(﹣16,﹣4).
,﹣4)或(﹣16,﹣4).
【解析】
(1)当x=1时,y=![]() x﹣
x﹣![]() ,即点C的坐标为(1,-4),将点C的坐标代入直线l1:y=-x+b中,即可求直线l1解析式;再根据P点纵坐标为2,求出P点坐标,然后求出直线AC的解析式,因为直线AC交y轴于点M,所以M横坐标为0,再求出纵坐标,最后根据S△CPQ=
,即点C的坐标为(1,-4),将点C的坐标代入直线l1:y=-x+b中,即可求直线l1解析式;再根据P点纵坐标为2,求出P点坐标,然后求出直线AC的解析式,因为直线AC交y轴于点M,所以M横坐标为0,再求出纵坐标,最后根据S△CPQ=![]() QM×(xC﹣xP)=
QM×(xC﹣xP)=![]() =5,解得:yQ=0或-5,即可得出结果;(2)根据最短路径问题可得:作C关于过A垂线的对称点C′(﹣7,﹣4)、A关于y轴的对称点A′(3,0),连接A′C′交过A点的垂线与点P,交y轴于点Q,此时,CP+PQ+QA的值最小,解得直线A′C′的表达式,从而求得点P的坐标;(3)如图2,点E的坐标为(-2,0),将直线l1绕点C逆时针旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标;若不存在,请说明理由.
=5,解得:yQ=0或-5,即可得出结果;(2)根据最短路径问题可得:作C关于过A垂线的对称点C′(﹣7,﹣4)、A关于y轴的对称点A′(3,0),连接A′C′交过A点的垂线与点P,交y轴于点Q,此时,CP+PQ+QA的值最小,解得直线A′C′的表达式,从而求得点P的坐标;(3)如图2,点E的坐标为(-2,0),将直线l1绕点C逆时针旋转,使旋转后的直线l3刚好过点E,过点C作平行于x轴的直线l4,点M、N分别为直线l3、l4上的两个动点,是否存在点M、N,使得△BMN是以M点为直角顶点的等腰直角三角形,若存在,直接写出N点的坐标;若不存在,请说明理由.
(1)直线l2:y=![]() x﹣
x﹣![]() ,令x=1,则y=﹣4,故C(1,﹣4),
,令x=1,则y=﹣4,故C(1,﹣4),
把C(1,﹣4)代入直线l1:y=﹣x+b,得:b=﹣3,则l1为:y=﹣x﹣3, 所以A(﹣3,0),所以点P坐标为(﹣3,2),如图,设直线AC交y轴于点M,
设yPC=mx+t得:![]() ,解得
,解得![]() , ∴yPC=-1.5x-2.5,即M(0,-2.5).
, ∴yPC=-1.5x-2.5,即M(0,-2.5).
S△CPQ=![]() QM×(xC﹣xP)=
QM×(xC﹣xP)=![]() =5,解得:yQ=0或-5,
=5,解得:yQ=0或-5,
∴Q的坐标为(0,0)或(0,
(2)确定C关于过A垂线的对称点C′(﹣7,﹣4)、A关于y轴的对称点A′(3,0),
连接A′C′交过A点的垂线与点P,交y轴于点Q,此时,CP+PQ+QA的值最小,
将点A′、C′点的坐标代入一次函数表达式:y=k′x+b′得:![]() ,解得:
,解得: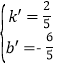 ,
,
则直线A′C′的表达式为:y=![]() x﹣
x﹣![]() ,当x=﹣3时,y=﹣
,当x=﹣3时,y=﹣![]() ,
,
即点P的坐标为(﹣3,﹣![]() ),
),
(3)将E、C点坐标代入一次函数表达式,同理可得其表达式为![]()
①当点M在直线l4上方时,设点N(n,﹣4),点M(s,﹣![]() s﹣
s﹣![]() ),点B(4,0),
),点B(4,0),
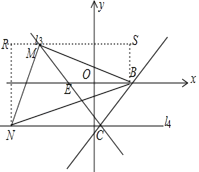
过点N、B分别作y轴的平行线交过点M与x轴的平行线分别交于点R、S,
∵∠RMN+∠RNM=90°,∠RMN+∠SMR=90°,
∴∠SMR=∠RNM,
∠MRN=∠MSB=90°,MN=MB,
∴△MSB≌△NRM(AAS),
∴RN=MS,RM=SB,
即![]()
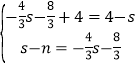 ,解得
,解得![]()
故点N的坐标为(﹣16,﹣4),
②当点M在l4下方时,如图1,过点M作PQ∥x轴,与过点B作y轴的平行线交于Q,与过点N作y轴的平行线交于P,
同①的方法得,N(﹣![]() ,﹣4),
,﹣4),
即:点N的坐标为(﹣![]() ,﹣4)或(﹣16,﹣4).
,﹣4)或(﹣16,﹣4).