题目内容
【题目】关于x的方程组
的解满足x为负数，y为正数，
（1）求 k的取值范围．
（2）化简｜k+5｜+｜k-3｜
【答案】（1）k＞-4；（2）｜k+5｜+｜k-3｜=8.
【解析】
（1）利用加减消元法解二元一次方程组，用含k的代数式分别表示x、y；再利用x为负数，y为正数，即可求得k的取值范围；
（2）利用（1）求得的k的取值范围，化简绝对值即可.
解：（1）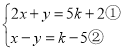
①+②得，3x=6k-3
解得x=2k-1，
代入②解得y=k+4，
∵x为负数，y为正数，
∴2k-1＜0，k+4＞0
由2k-1＜0解得，k＜
，
由k+4＞0解得，k＞-4，
所以，k的取值范围是-4＜k＜；
（2）∵-4＜k＜；
∴k+5＞0，k-3＜0
∴｜k+5｜+｜k-3｜=（k+5）+[-（k-3）]= k+5+3-k=8
练习册系列答案
小学课时特训系列答案
相关题目
