题目内容
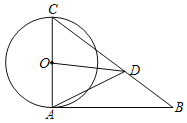
【题目】如图,△ABC中,AC为⊙O的直径,点D在BC上,AC=CD,∠ACB=2∠BAD
(1)求证:AB与⊙O相切;
(2)连接OD,若tanB=![]() ,求tan∠ADO.
,求tan∠ADO.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)设线段AD与⊙O交于E,连接CE,根据AC为⊙O的直径,可得CE⊥AD,再根据等腰三角形三线合一的性质可得∠ACD=2∠ACE,根据∠ACB=2∠BAD,从而得出∠ACE=∠DAB,再根据∠CAE=90°,可推出∠CAB=90°,即可证明AB与⊙O相切;
(2)延长CE交AB于M,则CM为AD的垂直平分线,连接DM,通过证明△ACM≌△DCM(SSS),可得∠BDM=90°,再根据锐角三角函数和中位线的性质求解即可.
(1)证明:设线段AD与⊙O交于E,连接CE,
∵AC为⊙O的直径,
∴CE⊥AD,
∵AC=CD,
∴∠ACD=2∠ACE,
∵∠ACB=2∠BAD,
∴∠ACE=∠DAB,
∵∠CAE=90°,
∴∠CAE+∠DAB=90,
∴∠CAB=90°,
∴AB与⊙O相切;
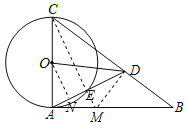
(2)解:∵AB与⊙O相切,
∴∠CAB=90°,
延长CE交AB于M,则CM为AD的垂直平分线,连接DM,
∴DM=AM,
∵AC=CD,CM=CM,
∴△ACM≌△DCM(SSS),
∴∠CDM=∠CAB=90°,
∴∠BDM=90°,
∵tanB=![]() ,
,
∴设AM=MD=3a,DB=4a,MB=5a,
AB=8a,AC=6a,
∴tan∠ACM=tan∠EAM=![]() ,
,
∴CE=2AE,AE=2EM,
设EN=k,
∴AE=DE=2k,CE=4k,
过O作ON⊥AD于N,
∴ON∥CE,
∴ON=![]() CE=2k,AN=
CE=2k,AN=![]() AE=k,
AE=k,
∴DN=3AN=3k,
∴tan∠ADO=![]() =
=![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目