题目内容
【题目】已知数轴上两点![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,且满足
,且满足![]() ,
,![]() 为原点.
为原点.
(1)试求![]() 和
和![]() 的值;
的值;
(2)点![]() 从
从![]() 点出发向右运动,经过3秒后点
点出发向右运动,经过3秒后点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点距离的3倍,求点
点距离的3倍,求点![]() 的运动速度?
的运动速度?
(3)点![]() 以一个单位每秒的速度从点
以一个单位每秒的速度从点![]() 向右运动,同时点
向右运动,同时点![]() 从点
从点![]() 出发以5个单位每秒的速度向左运动,点
出发以5个单位每秒的速度向左运动,点![]() 从点
从点![]() 出发,以20个单位每秒的速度向右运动.在运动过程中,
出发,以20个单位每秒的速度向右运动.在运动过程中,![]() 分别为
分别为![]() 的中点,问
的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
【答案】(1)![]() ;(2)2个单位/秒或5个单位/秒;(3)
;(2)2个单位/秒或5个单位/秒;(3)![]() 的值不发生变化,其值为2,理由见解析.
的值不发生变化,其值为2,理由见解析.
【解析】
(1)利用非负数的性质求解;
(2)设点![]() 运动的速度为v个单位/秒,则3s后点
运动的速度为v个单位/秒,则3s后点![]() 表示的数为3v,AC=3v+3,再分点C在点B的左侧或右侧两种情况,列方程即可求解;
表示的数为3v,AC=3v+3,再分点C在点B的左侧或右侧两种情况,列方程即可求解;
(3)设运动的时间为![]() ,根据题意用t表示出PQ,OD,MN的长,进而求出答案.
,根据题意用t表示出PQ,OD,MN的长,进而求出答案.
解:(1)∵|a+3|+(b-9)2020=0,
∴a+3=0且b-9=0,
∴a=-3,b=9;
(2)设点![]() 运动的速度为v个单位/秒,则3s后点
运动的速度为v个单位/秒,则3s后点![]() 表示的数为3v,
表示的数为3v,
又由(1)知,点A表示的数为-3,点B表示的数为9,
∴![]() ,
,
当点C在点B左侧时,BC=9-3v,则![]() ,解得v=2;
,解得v=2;
当点C在点B右侧时,BC=3v-9,则![]() ,解得v=5,
,解得v=5,
故点C的运动速度为2个单位/秒或5个单位/秒;
(3)![]() 的值不发生变化,理由如下:
的值不发生变化,理由如下:
设运动的时间为![]() ,则
,则![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,
又![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,
∴![]() 表示的数为
表示的数为![]() ,
,![]() 表示的数为
表示的数为![]() ,
,
∴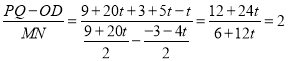 .
.
即![]() 的值不发生变化,其值为2.
的值不发生变化,其值为2.

【题目】某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | 种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.